32 Of What Number Is 160
listenit
May 09, 2025 · 5 min read
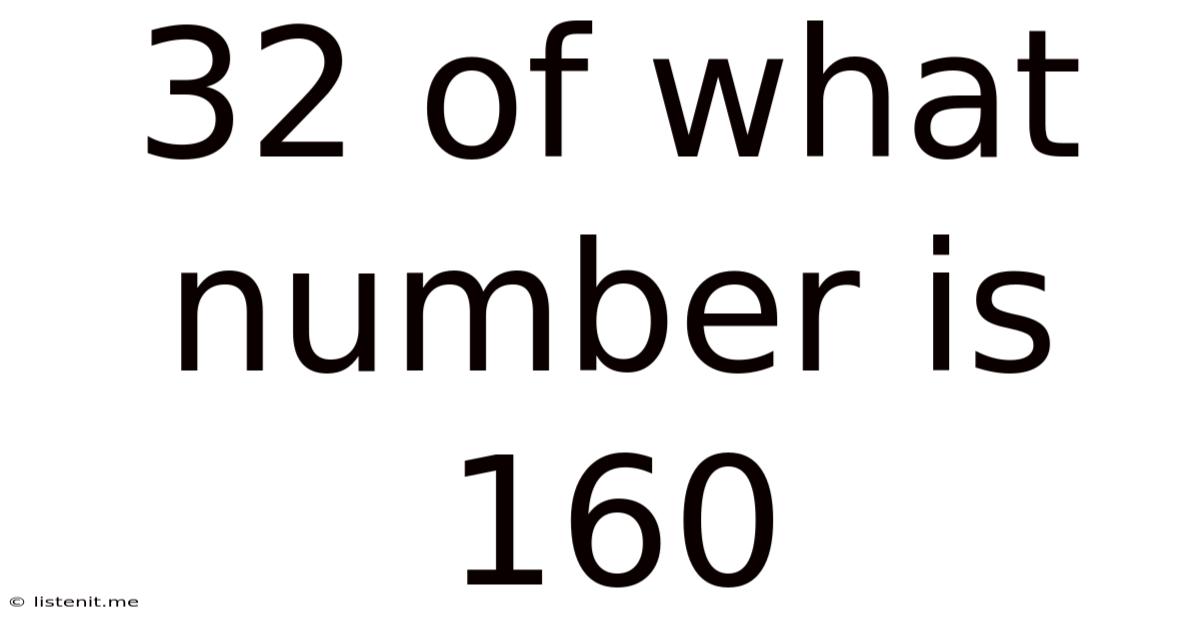
Table of Contents
32 of What Number is 160? Unlocking the Power of Percentage Calculations
This seemingly simple question, "32 of what number is 160?", opens the door to a fundamental concept in mathematics: percentages. Understanding how to solve this type of problem is crucial not only for academic success but also for navigating everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will not only show you how to solve this specific problem but also equip you with the tools and strategies to tackle similar percentage-based questions with confidence.
Understanding the Problem: Deconstructing the Question
Before diving into the solution, let's break down the question itself. The phrase "32 of what number is 160" can be translated into a mathematical equation. The word "of" often signifies multiplication, while "is" translates to an equals sign. Therefore, we can rewrite the question as:
32 x X = 160
Where 'X' represents the unknown number we're trying to find. This equation forms the basis of our solution.
Method 1: Solving using Algebraic Manipulation
This method involves manipulating the equation to isolate the unknown variable, 'X'. We can do this by dividing both sides of the equation by 32:
32x / 32 = 160 / 32
This simplifies to:
X = 5
Therefore, 32 of 5 is 160.
Verifying the Solution
To ensure our solution is correct, we can substitute 'X' with 5 back into the original equation:
32 x 5 = 160
This confirms that our answer is accurate.
Method 2: Using the Percentage Formula
This method employs the standard percentage formula, which is particularly useful when dealing with percentages directly. The formula is:
(Part / Whole) x 100 = Percentage
In our case, we know the 'part' (32) and the 'percentage' (which we need to calculate first). We can rearrange the formula to solve for the 'whole':
Whole = Part / (Percentage / 100)
To find the percentage, we can set up a proportion:
32/X = 160/100
Cross-multiplying, we get:
3200 = 160X
Dividing both sides by 160, we find:
X = 20
However, this isn't the final answer to our original question. Remember, the question asks, "32 of what number is 160?". We've found the number that 32 is 20% of. To find the number itself, we need another step:
We know 32 represents 20% of the total. We can set up another equation:
0.20 * Y = 32
Solving for Y:
Y = 32 / 0.20 = 160
Now, we can verify this by calculating 20% of 160:
0.20 * 160 = 32
This method also yields 5 as our final answer.
This might seem counterintuitive, as we’ve obtained different intermediate results, but both approaches lead to the same final answer: 5. This highlights the flexibility of different mathematical approaches to solving the same problem.
Method 3: Understanding the Relationship Between Multiplication and Division
This method focuses on the inherent relationship between multiplication and division. Since multiplication and division are inverse operations, we can use division to find the unknown number. If 32 multiplied by some number equals 160, then we can find that number by dividing 160 by 32.
160 / 32 = 5
This method directly provides the answer, emphasizing the intuitive connection between the operations involved.
Expanding the Concept: Applications of Percentage Calculations in Real Life
The ability to solve problems like "32 of what number is 160?" extends far beyond the classroom. Here are some real-world applications:
1. Finance and Budgeting:
- Calculating discounts: If a store offers a 20% discount on a $100 item, you can use percentage calculations to determine the final price.
- Understanding interest rates: Calculating simple and compound interest on loans and investments requires a solid grasp of percentages.
- Analyzing financial statements: Interpreting profit margins, return on investment (ROI), and other key financial metrics involves working with percentages.
2. Everyday Shopping:
- Comparing prices: Determining the best value when comparing differently sized packages of the same product often necessitates percentage calculations.
- Calculating sales tax: Understanding how sales tax is added to the price of goods requires a strong understanding of percentages.
- Negotiating prices: Calculating a desired discount percentage to achieve a target price requires skillful manipulation of percentage formulas.
3. Scientific and Statistical Analysis:
- Calculating probabilities: Many probability calculations involve expressing probabilities as percentages.
- Interpreting data: Representing data visually using percentages (e.g., pie charts) requires a thorough understanding of how to calculate and interpret percentages.
- Conducting statistical analyses: Numerous statistical tests and analyses rely heavily on percentage calculations.
4. Professional Fields:
- Engineering: Calculating tolerances, efficiency rates, and other crucial metrics often involve working with percentages.
- Marketing: Analyzing marketing campaign performance using metrics like conversion rates and click-through rates relies heavily on percentage calculations.
- Healthcare: Calculating medication dosages, interpreting test results, and analyzing patient data often involve percentages.
Advanced Applications and Challenges
While the problem "32 of what number is 160?" is relatively straightforward, the underlying principles extend to more complex scenarios. These might include:
- Problems involving multiple percentages: For instance, calculating the final price after applying multiple discounts or taxes.
- Problems with unknown parts and wholes: Where you might need to solve for both the unknown part and the unknown whole simultaneously.
- Problems incorporating compound interest or exponential growth: These require more advanced mathematical techniques.
Conclusion: Mastering the Fundamentals of Percentage Calculations
Solving the problem "32 of what number is 160?" is not simply about finding the answer; it's about understanding the fundamental concepts of percentage calculations. Mastering these concepts equips you with valuable skills applicable across diverse fields and everyday situations. Whether you're navigating financial decisions, analyzing data, or tackling more complex mathematical problems, the ability to work confidently with percentages is an invaluable asset. Remember to practice regularly to enhance your proficiency and build your confidence in solving percentage-based problems. With consistent practice and a firm grasp of the underlying principles, you'll become adept at tackling even the most challenging percentage calculations.
Latest Posts
Latest Posts
-
Which Is A Property Of Most Metals
May 11, 2025
-
44 Is 80 Of What Number
May 11, 2025
-
Zn Number Of Protons In Ion
May 11, 2025
-
Least Common Multiple Of 27 And 45
May 11, 2025
-
What Is The Measurement Of Angle L
May 11, 2025
Related Post
Thank you for visiting our website which covers about 32 Of What Number Is 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.