3 X 3 - 3 Divided By 3 + 3
listenit
May 26, 2025 · 5 min read
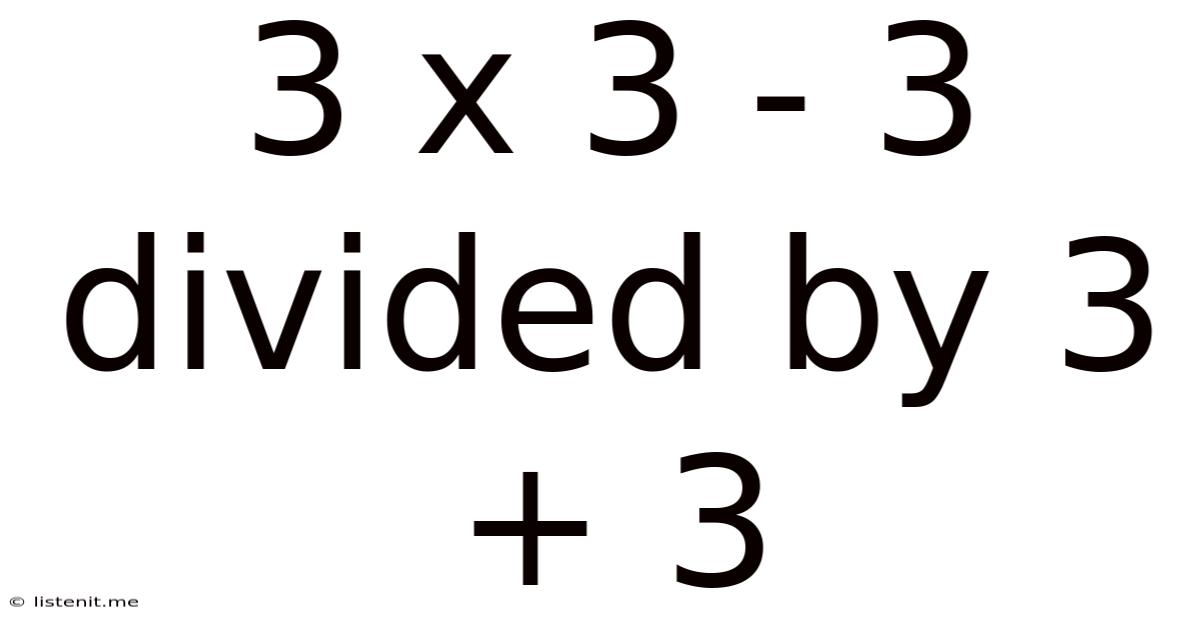
Table of Contents
Unraveling the Mystery: A Deep Dive into 3 x 3 - 3 ÷ 3 + 3
The seemingly simple mathematical expression "3 x 3 - 3 ÷ 3 + 3" has ignited countless debates and discussions online. Its deceptive simplicity masks a crucial understanding of the order of operations, a fundamental concept in mathematics. This article will not only solve the equation but will also delve into the underlying principles, explore common pitfalls, and offer practical applications to enhance your mathematical understanding.
Understanding the Order of Operations (PEMDAS/BODMAS)
Before tackling the equation, it's crucial to understand the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same hierarchical structure:
- Parentheses/Brackets: Calculations within parentheses or brackets are performed first.
- Exponents/Orders: Exponents (powers) are calculated next.
- Multiplication and Division: Multiplication and division are performed from left to right. They hold equal precedence.
- Addition and Subtraction: Addition and subtraction are performed from left to right. They also hold equal precedence.
Solving the Equation: 3 x 3 - 3 ÷ 3 + 3
Now, armed with the knowledge of the order of operations, let's solve the equation step-by-step:
-
Multiplication and Division (from left to right):
- 3 x 3 = 9
- 3 ÷ 3 = 1
-
Substitution: Replace the multiplication and division parts of the original equation with their results:
- 9 - 1 + 3
-
Addition and Subtraction (from left to right):
- 9 - 1 = 8
- 8 + 3 = 11
Therefore, the solution to 3 x 3 - 3 ÷ 3 + 3 is 11.
Common Mistakes and Misinterpretations
Many errors arise from neglecting the order of operations. Some common mistakes include:
- Performing operations from left to right without considering precedence: This would lead to an incorrect answer: 3 x 3 = 9, 9 - 3 = 6, 6 ÷ 3 = 2, 2 + 3 = 5. This is incorrect because it ignores the precedence of multiplication and division over addition and subtraction.
- Misunderstanding the equal precedence of multiplication/division and addition/subtraction: This leads to arbitrary order selections, yielding incorrect results. Remember, operations with equal precedence are performed from left to right.
- Incorrect use of calculators: Some basic calculators might not follow the correct order of operations. Always double-check your results, especially with complex expressions.
Beyond the Basics: Practical Applications and Extensions
The order of operations isn't just an abstract mathematical concept; it's essential for various practical applications:
1. Programming and Computer Science
In programming, the order of operations is crucial for writing correct and efficient code. Programming languages strictly adhere to the order of operations, and neglecting it can lead to unexpected program behavior and errors. Consider how this affects complex calculations in software, simulations, and data analysis. For example, a simple formula in a spreadsheet program will utilize the order of operations.
2. Physics and Engineering
Many physical formulas and engineering calculations rely heavily on the order of operations. From calculating forces and velocities to determining electrical currents and resistances, the correct order ensures accurate results and reliable designs. Think about the implications of a miscalculation in a bridge design or a space mission trajectory.
3. Finance and Accounting
Financial calculations frequently involve multiple operations. Compound interest, investment returns, and profit/loss calculations all require a precise understanding of the order of operations to produce accurate financial statements and analyses. An error in a financial model could have significant consequences.
4. Everyday Life
While not always explicitly stated, the order of operations underlies many everyday calculations. For instance, calculating the total cost of groceries, determining the remaining balance after a series of transactions, or even figuring out the final score in a sporting event involves applying these principles implicitly.
Expanding the Equation: Introducing Variables and Parentheses
Let's explore how the equation changes when we introduce variables and parentheses:
Example 1: Introducing Variables
Let's replace the number 3 with variables:
a x b - c ÷ d + e
To solve this equation, we would substitute the values of a, b, c, d, and e and follow the order of operations as previously outlined.
Example 2: Adding Parentheses
Parentheses dramatically alter the order of operations:
(3 x 3) - (3 ÷ 3) + 3
Here, the parentheses force us to perform the calculations inside the parentheses first:
- (3 x 3) = 9
- (3 ÷ 3) = 1
Then, we proceed with the remaining operations:
- 9 - 1 = 8
- 8 + 3 = 11
This example shows that even a slight change in parentheses can affect the result. Note that this specific example yields the same final answer, but that is not always the case.
Example 3: A More Complex Equation
Consider a more complex expression:
2 + (5 x (4 - 2) ÷ 2) + 6
- Innermost Parentheses: (4 - 2) = 2
- Multiplication Inside Parentheses: 5 x 2 = 10
- Division Inside Parentheses: 10 ÷ 2 = 5
- Outer Parentheses: 2 + 5 + 6
- Addition: 2 + 5 + 6 = 13
The result is 13. This demonstrates how parentheses dictate the order of calculations, leading to a different outcome from a similar expression without parentheses.
Conclusion: Mastering the Order of Operations
The equation "3 x 3 - 3 ÷ 3 + 3" serves as a microcosm of the broader importance of understanding the order of operations. It's a fundamental principle underlying nearly all areas of mathematics and its applications. By mastering the order of operations (PEMDAS/BODMAS) and understanding its implications, you equip yourself with a crucial tool for accurate calculations and problem-solving in numerous contexts – from everyday tasks to advanced scientific and engineering endeavors. Remember to always prioritize parentheses, then exponents, followed by multiplication and division (left to right), and finally addition and subtraction (left to right). With practice, this seemingly simple concept becomes second nature, enhancing your mathematical skills significantly.
Latest Posts
Latest Posts
-
Optics And Laser Technology Impact Factor
May 27, 2025
-
The American Journal Of Emergency Medicine
May 27, 2025
-
Forest Ecology And Management Journal Impact Factor
May 27, 2025
-
Sustainable Cities And Society Impact Factor
May 27, 2025
-
Energy Conversion And Management Impact Factor
May 27, 2025
Related Post
Thank you for visiting our website which covers about 3 X 3 - 3 Divided By 3 + 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.