3 To The Second Power Equals
listenit
May 24, 2025 · 5 min read
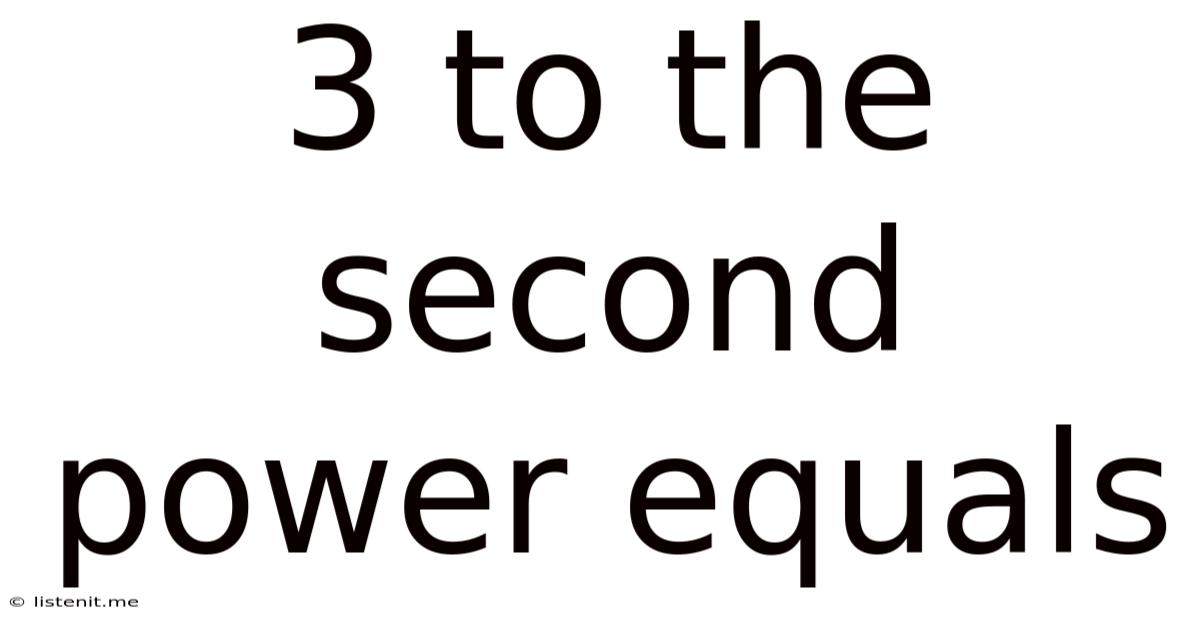
Table of Contents
3 to the Second Power Equals: Unveiling the Fundamentals of Exponents
The seemingly simple statement, "3 to the second power equals," opens a door to a vast world of mathematical concepts. Understanding this fundamental principle is crucial for anyone venturing into algebra, calculus, and beyond. This comprehensive guide will delve into the meaning of exponents, explore the specific case of 3 squared, demonstrate its applications, and address common misconceptions. We'll also touch upon the broader implications of exponents in various fields, from computer science to finance.
Understanding Exponents: A Foundation in Mathematics
Before diving into the specifics of 3 to the second power, let's establish a solid understanding of exponents themselves. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's written as a superscript to the right of the base. For example:
- x²: This means 'x' multiplied by itself twice (x * x).
- x³: This means 'x' multiplied by itself three times (x * x * x).
- xⁿ: This means 'x' multiplied by itself 'n' times.
The base (x) can be any number, variable, or even an expression. The exponent (n) is usually a positive integer, but it can also be negative, zero, or even a fraction (which leads to roots and fractional powers).
3 to the Second Power: The Calculation and its Meaning
Now, let's address the question at hand: "3 to the second power equals?" This is written as 3². Applying the definition of exponents, we have:
3² = 3 * 3 = 9
Therefore, 3 to the second power equals 9. This is also commonly referred to as "3 squared" because it represents the area of a square with sides of length 3 units.
Visualizing 3 Squared: The Geometric Interpretation
The concept of 3 squared can be easily visualized geometrically. Imagine a square with sides of length 3 units. To find the area of this square, you would multiply the length of one side by the length of the other side (3 * 3 = 9 square units). This simple geometric representation helps to solidify the understanding of exponents and their practical applications.
Beyond 3 Squared: Exploring Other Exponents
Understanding 3² lays a foundation for grasping more complex exponential expressions. Let's explore some related examples:
- 3 to the first power (3¹): This simply equals 3. Any number raised to the power of 1 is itself.
- 3 to the third power (3³): This is 3 * 3 * 3 = 27. This represents the volume of a cube with sides of length 3 units.
- 3 to the zero power (3⁰): This equals 1. Any non-zero number raised to the power of 0 is always 1. This might seem counterintuitive, but it's a fundamental rule of exponents.
- 3 to the negative second power (3⁻²): This equals 1/(3²) = 1/9. Negative exponents represent reciprocals.
Applications of Exponents: A Wide Range of Fields
The concept of exponents is not confined to abstract mathematical exercises. It has far-reaching applications in numerous fields, including:
1. Computer Science:
- Data storage: Data storage capacity is often expressed in powers of 2 (kilobytes, megabytes, gigabytes, etc.). Understanding exponents is essential for working with binary systems and calculating storage needs.
- Algorithm complexity: The efficiency of computer algorithms is frequently analyzed using Big O notation, which involves exponential functions to describe the growth of computation time with increasing input size.
2. Finance:
- Compound interest: Compound interest calculations rely heavily on exponential functions. Understanding exponential growth is vital for comprehending investment returns and loan repayments.
- Financial modeling: Sophisticated financial models often employ exponential functions to forecast future values, analyze risks, and optimize investment strategies.
3. Physics:
- Exponential decay: Many physical phenomena, such as radioactive decay and the cooling of objects, follow exponential decay patterns.
- Growth and decay equations: Exponential functions are used to model various growth and decay processes, including population growth, the spread of diseases, and chemical reactions.
4. Biology:
- Population growth: The growth of populations (bacteria, animals, etc.) can often be modeled using exponential functions.
- Drug concentration: The concentration of a drug in the bloodstream over time often follows an exponential decay pattern.
5. Engineering:
- Signal processing: Exponential functions are crucial in signal processing, used for analyzing and manipulating signals in various applications like communications and image processing.
- Structural analysis: Exponential functions might be employed in certain structural analysis calculations to determine stress and strain within materials.
Common Misconceptions About Exponents
Despite their apparent simplicity, exponents often lead to common misconceptions:
- Mistaking exponentiation for multiplication: It's crucial to remember that 3² is not 3 * 2, but 3 * 3. This is a fundamental difference that must be understood.
- Incorrect order of operations: When dealing with multiple operations, the order of operations (PEMDAS/BODMAS) must be followed correctly. Exponents come before multiplication and division.
- Misunderstanding negative and fractional exponents: Negative exponents represent reciprocals, and fractional exponents represent roots. A thorough understanding of these concepts is necessary to avoid errors.
Mastering Exponents: A Path to Mathematical Proficiency
Mastering exponents is a cornerstone of mathematical proficiency. It's not just about memorizing formulas; it's about understanding the underlying concepts and their applications. By grasping the fundamental principles, visualizing the geometric interpretations, and appreciating the wide range of applications, you can unlock a deeper understanding of mathematics and its power to model and explain the world around us. From calculating the area of a square to forecasting financial growth, the humble exponent plays a significant role in various fields, proving its importance in both theoretical and practical contexts. Continuously practicing and reinforcing your knowledge of exponents will empower you to tackle more complex mathematical challenges with confidence. Remember that consistent practice and exploration are key to mastering this foundational mathematical concept.
Latest Posts
Latest Posts
-
Lcm Of 2 6 And 11
May 24, 2025
-
14 Out Of 15 In Percentage
May 24, 2025
-
30 Days After November 15 2024
May 24, 2025
-
Common Factor Of 6 And 8
May 24, 2025
-
Least Common Multiple Of 9 12 And 18
May 24, 2025
Related Post
Thank you for visiting our website which covers about 3 To The Second Power Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.