3 Square Root Of 125 Simplified
listenit
May 12, 2025 · 4 min read
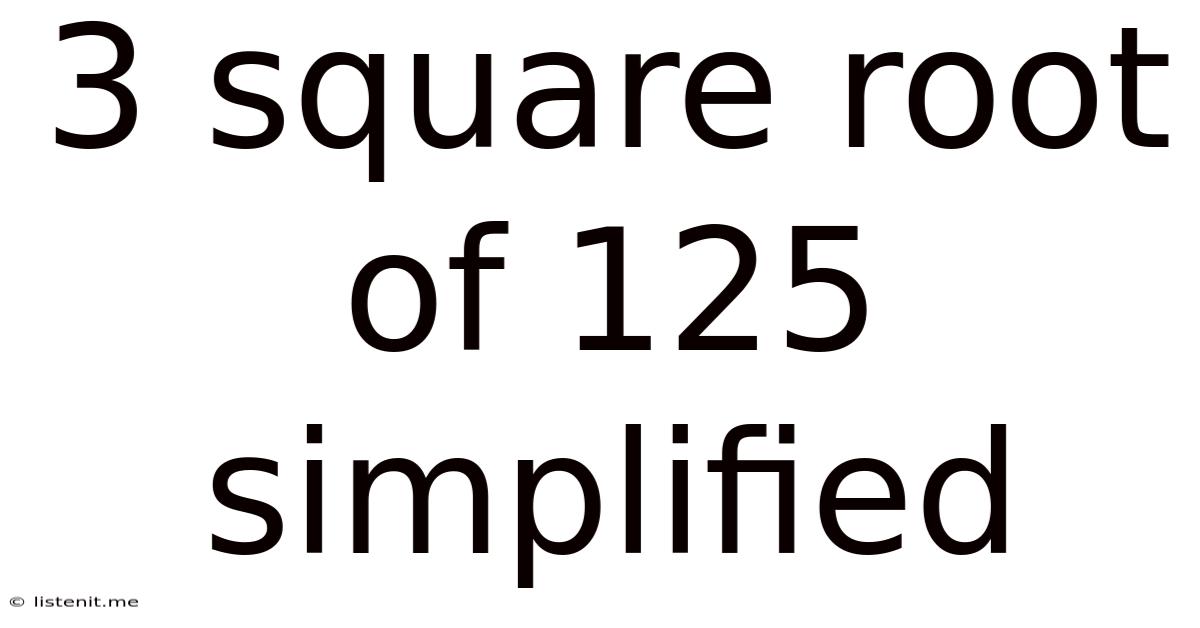
Table of Contents
3√125 Simplified: A Comprehensive Guide to Cube Roots and Simplification
Understanding cube roots and simplifying radical expressions is a fundamental skill in mathematics, particularly in algebra and calculus. This comprehensive guide delves into the simplification of the cube root of 125, offering a step-by-step process, exploring related concepts, and providing practical examples to solidify your understanding. We'll go beyond just finding the answer and explore the underlying principles that govern cube root simplification.
What is a Cube Root?
Before diving into the simplification of 3√125, let's establish a solid foundation by defining what a cube root is. A cube root is a number that, when multiplied by itself three times (cubed), equals a given number. In other words, if 'x' is the cube root of 'y', then x³ = y. The cube root is represented mathematically as ³√y or y^(1/3).
For instance:
- ³√8 = 2 because 2 x 2 x 2 = 8
- ³√27 = 3 because 3 x 3 x 3 = 27
- ³√64 = 4 because 4 x 4 x 4 = 64
Simplifying Cube Roots: The Fundamental Approach
Simplifying cube roots involves finding the largest perfect cube that divides the number under the radical sign (the radicand). A perfect cube is a number that results from cubing an integer (e.g., 8, 27, 64, 125, 216, etc.). The process involves factoring the radicand into its prime factors and then grouping them into sets of three.
Let's break down the steps with a few examples before tackling 3√125:
Example 1: Simplifying ³√24
- Prime Factorization: Find the prime factorization of 24. 24 = 2 x 2 x 2 x 3
- Grouping: Group the prime factors into sets of three: (2 x 2 x 2) x 3
- Simplification: Since (2 x 2 x 2) = 2³, we can take the cube root of this group, resulting in 2. The remaining factor, 3, stays under the cube root.
- Final Result: ³√24 = 2³√3
Example 2: Simplifying ³√108
- Prime Factorization: 108 = 2 x 2 x 3 x 3 x 3
- Grouping: (3 x 3 x 3) x 2 x 2
- Simplification: ³√(3 x 3 x 3) = 3. The remaining factors, 2 x 2 = 4, stay under the cube root.
- Final Result: ³√108 = 3³√4
Simplifying 3√125: A Step-by-Step Solution
Now, let's apply this method to simplify 3√125:
- Prime Factorization of 125: 125 = 5 x 5 x 5
- Grouping: We have a perfect cube: (5 x 5 x 5) = 5³
- Simplification: ³√(5 x 5 x 5) = 5
- Final Result: 3√125 = 5
Therefore, the simplified form of 3√125 is simply 5. This is because 5 cubed (5 x 5 x 5) equals 125.
Understanding the Concept of Perfect Cubes
The key to simplifying cube roots efficiently lies in identifying perfect cubes. Here's a list of some common perfect cubes:
- 1³ = 1
- 2³ = 8
- 3³ = 27
- 4³ = 64
- 5³ = 125
- 6³ = 216
- 7³ = 343
- 8³ = 512
- 9³ = 729
- 10³ = 1000
Becoming familiar with these perfect cubes will significantly speed up your simplification process. You can quickly recognize them within larger numbers, making the factoring and grouping steps more intuitive.
Advanced Simplification Techniques: Dealing with Variables
The simplification techniques we've discussed extend seamlessly to expressions involving variables. Let's consider an example:
Example: Simplifying ³√(8x³y⁶)
- Factorization: ³√(2³ x x³ x y⁶)
- Grouping: We group the factors into sets of three: ³√(2³ x x³ x (y²)³)
- Simplification: We can take the cube root of each group: 2xy²
- Final Result: ³√(8x³y⁶) = 2xy²
Practical Applications of Cube Roots and Simplification
Cube roots and their simplification aren't just abstract mathematical concepts; they have various practical applications in various fields:
- Geometry: Calculating the volume of cubes and other three-dimensional shapes often involves cube roots.
- Physics: Many physics formulas, especially those related to volume, density, and energy, utilize cube roots.
- Engineering: Cube roots are essential in structural calculations and designing various engineering structures.
- Chemistry: Cube roots are used in calculations related to molarity and concentrations in chemical solutions.
Troubleshooting Common Mistakes
When simplifying cube roots, several common mistakes can occur:
- Incorrect Prime Factorization: Double-check your prime factorization to ensure accuracy. An incorrect factorization will lead to an incorrect simplified form.
- Ignoring Perfect Cubes: Make sure you've identified and extracted all the perfect cubes from the radicand. Leaving any perfect cube inside the radical sign means the simplification is incomplete.
- Incorrect Grouping: Ensure you're correctly grouping the factors into sets of three when dealing with cube roots.
Conclusion: Mastering Cube Root Simplification
Mastering the simplification of cube roots, such as 3√125, is crucial for success in various mathematical and scientific fields. By understanding the fundamental principles of prime factorization, perfect cubes, and the step-by-step simplification process, you can confidently tackle more complex radical expressions. Remember to practice regularly, focusing on identifying perfect cubes and efficiently extracting them from the radicand. This will not only improve your speed and accuracy but also strengthen your overall mathematical abilities. Regular practice and a thorough understanding of the underlying principles will make you proficient in simplifying even the most challenging cube root expressions.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 Square Root Of 125 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.