3 Less Than The Square Of A Number.
listenit
May 09, 2025 · 5 min read
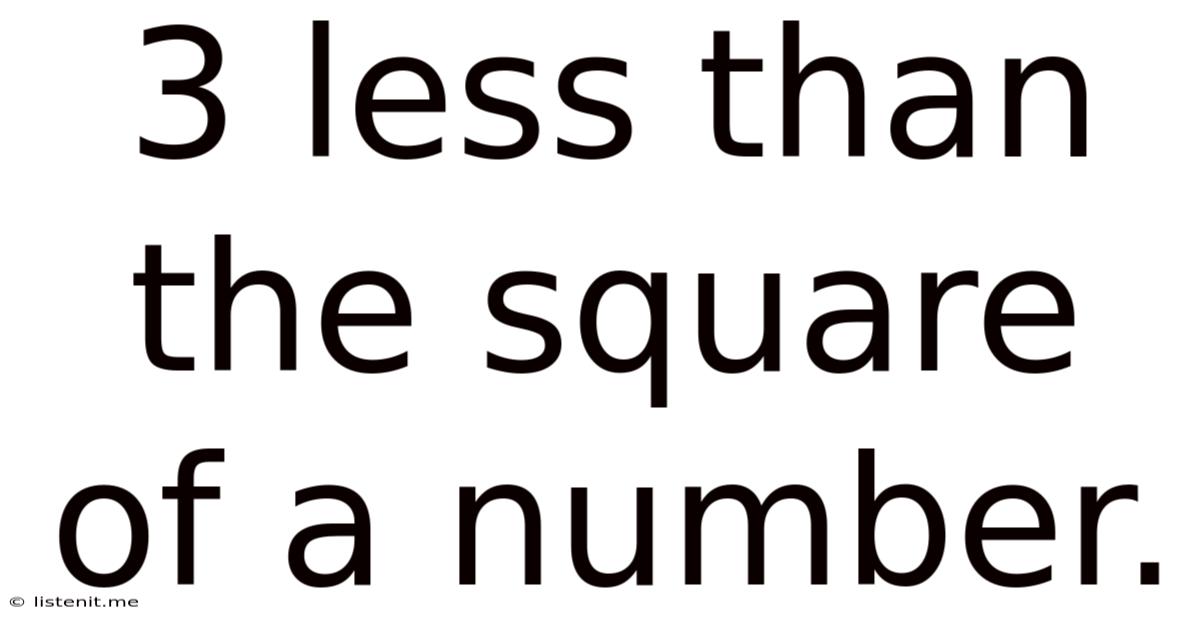
Table of Contents
3 Less Than the Square of a Number: A Deep Dive into Quadratic Expressions
The seemingly simple phrase "3 less than the square of a number" hides a world of mathematical richness. This seemingly straightforward expression opens doors to exploring quadratic equations, their graphs, applications in real-world scenarios, and the fascinating interplay between algebra and geometry. Let's delve into this seemingly simple concept and uncover its multifaceted nature.
Understanding the Expression: Algebraic Representation
Mathematically, "3 less than the square of a number" translates directly into an algebraic expression. Let's represent "a number" with the variable x. Then, the square of the number is x². Subtracting 3 from this gives us the expression:
x² - 3
This is a quadratic expression, characterized by the presence of a variable raised to the power of 2. Understanding this fundamental algebraic representation is the key to unlocking a deeper understanding of its implications.
Exploring the Quadratic Equation: Setting it Equal to Zero
While the expression x² - 3 is valuable on its own, setting it equal to zero transforms it into a quadratic equation:
x² - 3 = 0
Solving this equation reveals the values of x that satisfy the condition. We can solve this using various methods:
1. Solving by Factoring:
This equation isn't easily factorable using integers. However, understanding factoring is crucial for solving many other quadratic equations. For example, consider the equation x² - 4 = 0. This can be factored as (x - 2)(x + 2) = 0, leading to solutions x = 2 and x = -2.
2. Solving by the Quadratic Formula:
The quadratic formula is a powerful tool applicable to all quadratic equations of the form ax² + bx + c = 0. In our case, a = 1, b = 0, and c = -3. The quadratic formula is:
x = (-b ± √(b² - 4ac)) / 2a
Substituting our values, we get:
x = (0 ± √(0² - 4 * 1 * -3)) / (2 * 1)
x = ±√12 / 2
x = ±2√3 / 2
x = ±√3
Therefore, the solutions to the equation x² - 3 = 0 are x = √3 and x = -√3.
3. Solving by Completing the Square:
Completing the square is another method for solving quadratic equations. While less straightforward for this specific equation, it's a valuable technique for understanding the relationship between the equation and its graphical representation (discussed later).
Graphical Representation: Parabolas and Their Properties
The quadratic expression x² - 3 represents a parabola when graphed on a Cartesian coordinate system. A parabola is a U-shaped curve. The graph of y = x² - 3 is a parabola that opens upwards (because the coefficient of x² is positive).
-
Vertex: The vertex of the parabola is the lowest point (minimum value) on the graph. For y = x² - 3, the vertex is at (0, -3). This is because the parabola is a simple translation of the basic parabola y = x² three units downward.
-
x-intercepts: The x-intercepts are the points where the parabola intersects the x-axis (where y = 0). These are the solutions we found earlier using the quadratic formula: x = √3 and x = -√3.
-
y-intercept: The y-intercept is the point where the parabola intersects the y-axis (where x = 0). This is easily found by substituting x = 0 into the equation: y = 0² - 3 = -3. Therefore, the y-intercept is (0, -3), which is also the vertex in this case.
-
Axis of Symmetry: The parabola is symmetric about a vertical line passing through its vertex. This line of symmetry is given by the equation x = 0.
Real-World Applications: Where do we see this?
While seemingly abstract, quadratic expressions and equations have numerous real-world applications:
-
Physics: Projectile motion (the path of a thrown ball, for example) can be modeled using quadratic equations. The height of the projectile at any given time can be expressed as a quadratic function.
-
Engineering: Designing bridges, arches, and other structures often involves quadratic equations to determine optimal shapes and stress distributions.
-
Economics: Quadratic functions are used in economic modeling to represent cost functions, revenue functions, and profit functions.
-
Computer Graphics: Parabolas are used extensively in computer graphics to create curved shapes and smooth transitions.
Expanding the Concept: Variations and Extensions
Let's explore how modifying the expression "3 less than the square of a number" affects its algebraic and graphical representation.
Adding a Linear Term:
Consider the expression x² + 2x - 3. This adds a linear term (2x) to our original quadratic expression. This shifts the parabola both horizontally and vertically, altering the vertex, x-intercepts, and the overall shape of the graph. Solving the equation x² + 2x - 3 = 0 would yield different solutions.
Changing the Constant:
If we change the constant term, for example, to x² - 5, the parabola shifts vertically, changing its y-intercept and vertex. The x-intercepts would also change, representing different solutions to the equation x² - 5 = 0.
Multiplying by a Constant:
Multiplying the expression by a constant, such as 2x² - 6, stretches or compresses the parabola vertically. The x-intercepts remain the same, but the y-intercept and vertex change.
Conclusion: The Power of a Simple Expression
The expression "3 less than the square of a number," seemingly simple at first glance, opens a gateway to a deeper understanding of quadratic equations, their graphical representations, and their extensive real-world applications. By exploring its algebraic properties, solving its corresponding quadratic equation, and analyzing its graphical features, we uncover the rich mathematical landscape hidden within this concise phrase. From simple algebraic manipulations to solving complex equations and visualizing parabolas, this exploration highlights the beauty and power of mathematics in understanding and modeling the world around us. The seemingly simple expression provides a foundational understanding that extends far beyond its initial appearance, offering a stepping stone to more advanced mathematical concepts and real-world problem-solving.
Latest Posts
Latest Posts
-
At What Temperature Do Most Foodborne Pathogens Grow Most Quickly
May 09, 2025
-
What Group In The Periodic Table Is Least Reactive
May 09, 2025
-
Difference Between Average Atomic Mass And Mass Number
May 09, 2025
-
What Base Is Found On Rna Not Dna
May 09, 2025
-
What Is 70 As A Decimal
May 09, 2025
Related Post
Thank you for visiting our website which covers about 3 Less Than The Square Of A Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.