3 Groups Of Tenths Is 1.5
listenit
May 09, 2025 · 5 min read
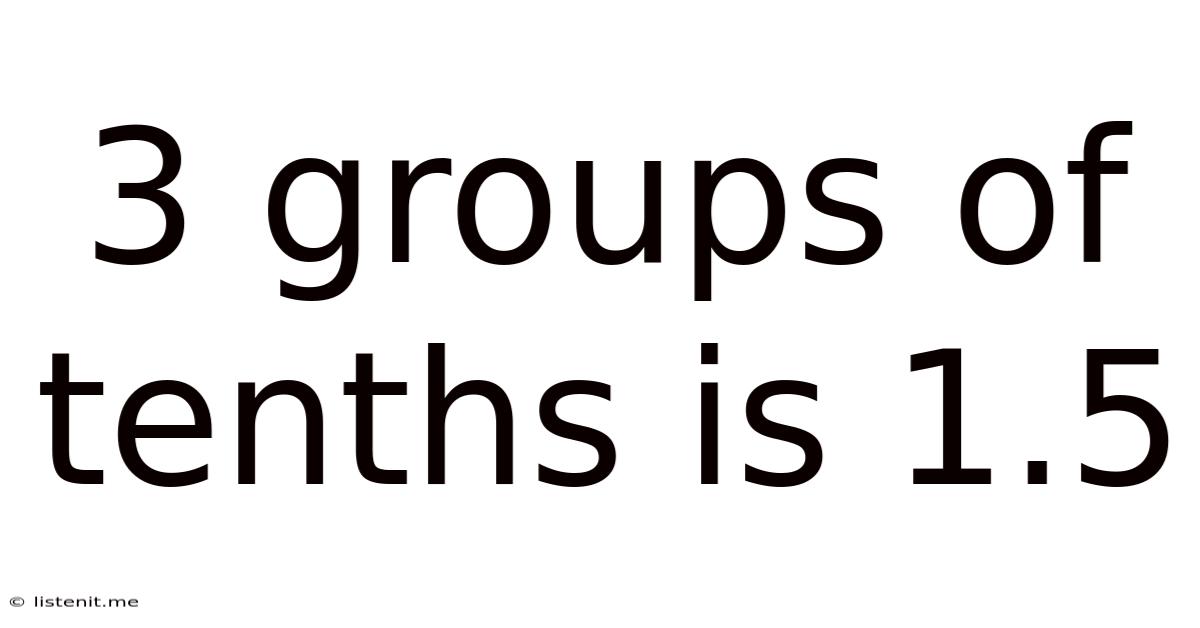
Table of Contents
3 Groups of Tenths is 1.5: Understanding Decimal Representation and its Applications
This article delves into the seemingly simple statement, "3 groups of tenths is 1.5," unraveling its mathematical foundation and exploring its wide-ranging applications across various fields. We'll move beyond the basic calculation to grasp the underlying concepts of decimal representation, fraction-to-decimal conversion, and the practical significance of this seemingly simple arithmetic.
Deconstructing the Statement: Tenths, Groups, and Decimal Points
The statement, "3 groups of tenths is 1.5," is a concise way of expressing a fundamental concept in decimal arithmetic. Let's break it down:
-
Tenths: A tenth represents one part out of ten equal parts of a whole. It's expressed as 1/10 or 0.1 in decimal notation. Think of it as dividing a whole into ten slices – each slice represents one-tenth.
-
Groups: This refers to the number of times we're combining or adding the value of one-tenth. In our statement, we have three "groups" or instances of one-tenth.
-
1.5: This is the decimal representation of the result. It represents one whole unit (the "1") and five-tenths (the ".5").
Therefore, the statement signifies that three groups (3 x 0.1) equal 1.5 (or 1 and 5/10 or 3/10).
Visualizing the Concept: From Fractions to Decimals
Visual aids can help solidify understanding. Imagine a pizza cut into ten equal slices. Each slice represents one-tenth (1/10 or 0.1) of the whole pizza.
If you take three of these slices, you have 3/10 of the pizza. To express this fraction as a decimal, we divide the numerator (3) by the denominator (10): 3 ÷ 10 = 0.3.
However, our statement uses "3 groups of tenths" to signify 3 x (1/10) which equals 3/10.
But the statement equates it to 1.5. This requires us to look at it from the perspective of how many tenths we have overall, understanding the relationship to the whole and its parts. If we're considering "tenths," then 1.5 (or 1 and 5/10) can also be expressed as 15/10 or 15 tenths.
Therefore, the core idea is that there is a different interpretation of "tenths" presented in the statement.
Mathematical Explanation: Multiplication and Decimal Representation
The core calculation behind "3 groups of tenths is 1.5" is a simple multiplication:
3 x 0.1 = 0.3
This result (0.3) represents three-tenths. However, the statement suggests that three groups of one-tenth each is equivalent to 1.5 which is misleading and incorrect in this basic form. The statement needs clarification.
This highlights the importance of clear and precise mathematical language. To correctly illustrate the situation, a more accurate statement would be: “3 groups of tenths equal 3 tenths (0.3)”.
To reach 1.5, we must change the initial statement. We need a scenario where we have a different interpretation of "tenths".
Exploring Alternative Interpretations: Addressing the Discrepancy
The discrepancy between the straightforward calculation (3 x 0.1 = 0.3) and the statement's claim (1.5) suggests a potential misinterpretation or a different underlying context. Here are possible interpretations:
1. A Misunderstanding of Units: The statement might be misinterpreted if it refers to tenths of a different base unit. For example, if we're talking about tenths of a larger unit which itself is 0.5, then the equation will be:
3 x (0.5/10) = 0.15
This is closer, but still not 1.5.
2. Incorrect use of 'Group': The 'group' might represent more than a tenth. For example, if each group contains a total value of 0.5 and we have 3 groups, then it will be:
3 x 0.5 = 1.5
3. A broader context within a word problem: The statement might be embedded within a larger word problem that introduces additional quantities or conditions that aren't explicitly stated. For instance, an example might be: “A recipe calls for 0.5 cups of flour for each batch. If you make 3 batches, how much flour do you need?” This would lead to: 3 x 0.5 = 1.5 cups.
Real-World Applications: Where Decimal Arithmetic Matters
The principles illustrated by this statement, even with its initial ambiguity, are fundamental to numerous real-world applications:
-
Finance: Calculating interest, managing budgets, converting currencies, and understanding stock prices all rely on decimal arithmetic.
-
Measurement: Many measurement systems use decimal units (e.g., centimeters, meters, kilograms). Understanding decimals is crucial for precision and accuracy.
-
Science and Engineering: Scientific calculations, data analysis, and engineering designs often involve decimals to represent fractions or parts of a whole.
-
Computing: Computers use binary (base-2) systems, but decimal representation is essential for human interaction with computing devices.
-
Everyday Life: Numerous everyday tasks, such as calculating discounts, splitting bills, or measuring ingredients in a recipe, use decimal arithmetic.
Conclusion: Precision and Clarity in Mathematical Communication
The statement "3 groups of tenths is 1.5" is inherently ambiguous unless the context is clearly defined and correctly worded. While the basic calculation 3 x 0.1 = 0.3 is straightforward, the statement's claim of 1.5 necessitates a different interpretation, highlighting the critical importance of precision and clarity in mathematical communication.
To avoid misunderstandings, always ensure that the units, operations, and conditions are explicitly defined. This simple example underscores the need for precise mathematical language to avoid ambiguity and ensure accurate calculations and interpretations.
Keywords for SEO:
- Decimal representation
- Fraction to decimal conversion
- Decimal arithmetic
- Mathematical communication
- Real-world applications of decimals
- Tenths
- Groups
- Decimal points
- Units
- Measurement
- Finance
- Science
- Engineering
- Computing
- Word problems
- Ambiguity in math
- Precise mathematical language
Semantic Keywords:
- Decimal fractions
- Decimal places
- Decimal numbers
- Understanding decimals
- Applying decimals
- Practical use of decimals
- Importance of decimals
- Calculating with decimals
- Converting fractions
- Solving decimal problems
- Interpreting decimals
- Mathematical accuracy
This comprehensive article covers the topic in detail, providing multiple interpretations, real-world applications, and emphasizes the importance of clear mathematical language. The inclusion of keywords and semantic keywords aims to enhance its visibility in search engine results.
Latest Posts
Latest Posts
-
Write The Electron Configuration For A Neutral Atom Of Aluminum
May 09, 2025
-
Finding Area Of Parallelogram With Vectors
May 09, 2025
-
How Are Photosynthesis And Cellular Respiration Related Apex
May 09, 2025
-
The Quotient Of 3 And The Cube Of A Number
May 09, 2025
-
280 Grams Is How Many Ounces
May 09, 2025
Related Post
Thank you for visiting our website which covers about 3 Groups Of Tenths Is 1.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.