3 5 Percent As A Decimal
listenit
May 10, 2025 · 5 min read
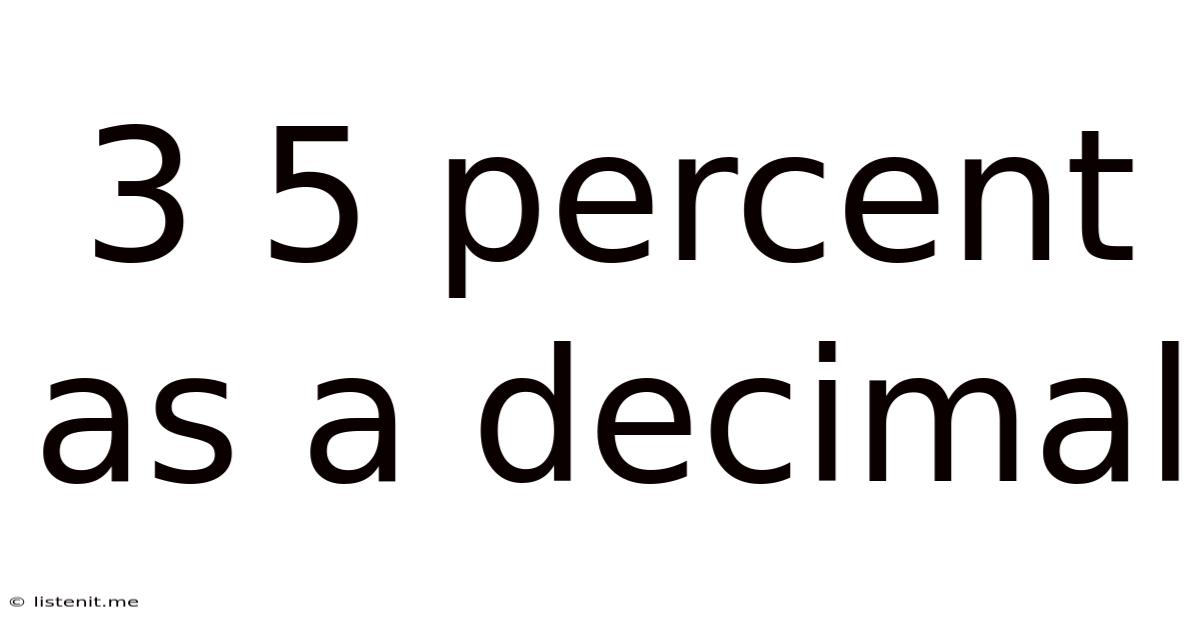
Table of Contents
3.5 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is fundamental to various fields, from finance and statistics to everyday calculations. This comprehensive guide will delve deep into the conversion of 3.5 percent to its decimal form, exploring the underlying principles and providing practical applications. We’ll also touch upon related concepts to ensure a complete understanding of this crucial mathematical skill.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." For example, 10% means 10 out of 100, or 10/100. This fraction can be simplified to 1/10.
Percentages are widely used to represent proportions, rates of change, and probabilities. They offer a convenient way to compare and understand different quantities, making them indispensable in various fields.
Converting Percentages to Decimals: The Core Concept
The conversion of a percentage to a decimal is a straightforward process. The key is to remember that a percentage is already a fraction with a denominator of 100. Therefore, to convert a percentage to a decimal, you simply divide the percentage by 100. This is equivalent to moving the decimal point two places to the left.
Let's illustrate this with a simple example: Consider 25%. To convert this to a decimal, we divide 25 by 100:
25/100 = 0.25
Alternatively, we can move the decimal point (implicitly located after the 25) two places to the left:
- → 0.25
Converting 3.5 Percent to a Decimal
Now, let's apply this knowledge to convert 3.5 percent to its decimal equivalent. Following the same procedure:
Method 1: Division
3.5 / 100 = 0.035
Method 2: Moving the Decimal Point
3.5% → 0.035
Therefore, 3.5% as a decimal is 0.035.
Practical Applications of Decimal Equivalents
Understanding the decimal equivalent of percentages is crucial in various real-world scenarios:
1. Financial Calculations:
-
Interest Rates: Banks and financial institutions use decimal representations of interest rates in their calculations. For example, an annual interest rate of 3.5% would be represented as 0.035 in interest calculations. This is essential for determining interest earned or paid on loans, investments, and savings accounts.
-
Discounts and Sales Tax: Many retail transactions involve discounts and sales tax. Converting percentage discounts or tax rates to decimals simplifies the calculations of final prices. For instance, a 3.5% sales tax on a purchase would be calculated using the decimal equivalent, 0.035.
-
Investment Returns: Investors routinely track their investment returns as percentages. Converting these percentages to decimals allows for easier comparison of returns from different investments.
2. Statistical Analysis:
-
Data Representation: In statistical analysis, data is often represented as percentages. Converting these percentages to decimals allows for easier manipulation and calculation of statistical measures like means, medians, and standard deviations.
-
Probability: Probability is frequently expressed as a percentage, representing the likelihood of an event occurring. Converting these percentages to decimals simplifies calculations involving probabilities.
3. Everyday Calculations:
-
Tips and Gratuities: Calculating tips or gratuities in restaurants often involves percentages. Converting the tip percentage to a decimal simplifies the calculation of the tip amount. For instance, a 3.5% tip on a bill can be calculated by multiplying the bill amount by 0.035.
-
Measurement Conversions: In certain situations, percentage changes in measurements need to be converted to decimals for easier comparison. This is applicable in fields like engineering and construction.
Expanding on the Concept: Dealing with Other Percentages
The principles discussed for converting 3.5% to a decimal apply to all percentages. Here are a few examples for further understanding:
- 100% as a Decimal: 100 / 100 = 1.00
- 50% as a Decimal: 50 / 100 = 0.50
- 12.5% as a Decimal: 12.5 / 100 = 0.125
- 0.5% as a Decimal: 0.5 / 100 = 0.005
- 250% as a Decimal: 250 / 100 = 2.50
Beyond the Basics: Working with Percentages and Decimals in Equations
Percentages and decimals are frequently used in mathematical equations. Understanding their inter-relationship is vital for accurate calculations. Here's a look at some examples:
-
Calculating a Percentage Increase: If a value increases by a certain percentage, you can calculate the new value by adding the percentage increase (as a decimal) to 1 and multiplying by the original value. For example, a 3.5% increase on a value of $100 would be calculated as: $100 * (1 + 0.035) = $103.50
-
Calculating a Percentage Decrease: Similarly, if a value decreases by a certain percentage, you can calculate the new value by subtracting the percentage decrease (as a decimal) from 1 and multiplying by the original value.
-
Finding the Percentage of a Value: To find a percentage of a value, simply multiply the value by the percentage (as a decimal). For example, to find 3.5% of 500, you would calculate: 500 * 0.035 = 17.5
Common Mistakes to Avoid
-
Forgetting to Divide by 100: A common mistake is forgetting to divide the percentage by 100 before converting to a decimal. Always remember this crucial step.
-
Incorrect Placement of the Decimal Point: When moving the decimal point, ensure it's moved two places to the left, not right.
-
Confusion with Fractions: While percentages are related to fractions, they are not directly interchangeable without conversion.
Conclusion: Mastering Percentages and Decimals
Mastering the conversion between percentages and decimals is a fundamental skill applicable in numerous contexts. Understanding the underlying principles and practicing the conversion method will enhance your mathematical proficiency and improve your ability to tackle problems in various fields. The ability to confidently convert 3.5 percent to its decimal equivalent, 0.035, is a small but significant step towards a deeper understanding of numerical concepts and their practical applications. Remember to practice regularly and apply this knowledge in real-world scenarios to reinforce your understanding. With consistent effort, you’ll gain fluency and confidence in handling percentages and decimals in all your calculations.
Latest Posts
Latest Posts
-
During Glycolysis Molecules Of Glucose Are
May 10, 2025
-
Burning Of Wood Is A Physical Change
May 10, 2025
-
What Determines The Direction Of Diffusion
May 10, 2025
-
What Is The Atomic Number Of Manganese
May 10, 2025
-
Do Flat Mirrors Produce Real Images
May 10, 2025
Related Post
Thank you for visiting our website which covers about 3 5 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.