3 5 Divided By 5 6
listenit
May 24, 2025 · 4 min read
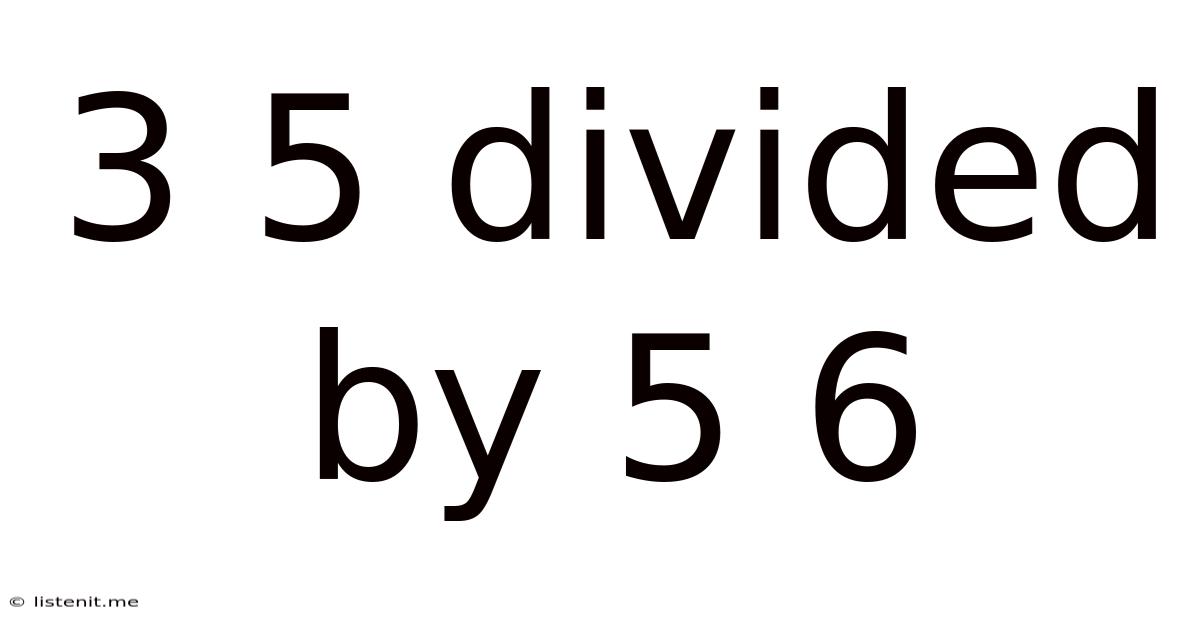
Table of Contents
Deconstructing 3.5 Divided by 5.6: A Deep Dive into Division
The seemingly simple mathematical expression "3.5 divided by 5.6" hides a wealth of underlying concepts. This article will explore this division problem in detail, examining not only the solution but also the broader mathematical principles involved, including significant figures, different methods of calculation, and real-world applications. We'll also delve into the importance of understanding division in various contexts and how to approach similar problems with confidence.
Understanding the Problem: 3.5 ÷ 5.6
At its core, the problem 3.5 ÷ 5.6 asks: "How many times does 5.6 fit into 3.5?" Intuitively, we know the answer will be less than 1, since the divisor (5.6) is larger than the dividend (3.5). This understanding is crucial before embarking on any calculation. The result will be a decimal number representing a fraction of 5.6.
Method 1: Long Division
Traditional long division offers a methodical approach to solving this problem. However, dealing with decimals necessitates careful placement of the decimal point.
-
Set up the division: Write 3.5 as the dividend and 5.6 as the divisor.
-
Adjust for decimals: Multiply both the dividend and divisor by 10 to remove the decimal point from the divisor, resulting in 35 ÷ 56.
-
Perform long division: The long division process involves repeatedly subtracting multiples of the divisor (56) from the dividend (35). Since 56 is larger than 35, the quotient will be less than 1. We add a decimal point and a zero to the dividend, making it 350. 56 goes into 350 approximately 6 times (56 x 6 = 336). Subtracting 336 from 350 leaves a remainder of 14.
-
Continue the process: Add another zero to the remainder, making it 140. 56 goes into 140 two times (56 x 2 = 112). Subtracting 112 from 140 leaves a remainder of 28. This process can be continued to achieve a higher level of accuracy.
-
Final result (approximation): Through long division, we get a quotient of approximately 0.625. The precision depends on how far you continue the long division process.
Method 2: Using Fractions
Converting decimals to fractions provides an alternative approach.
-
Convert decimals to fractions: 3.5 can be written as 35/10, and 5.6 can be written as 56/10.
-
Divide fractions: Dividing fractions involves inverting the second fraction (divisor) and multiplying. This gives us (35/10) * (10/56).
-
Simplify: The 10s cancel out, leaving 35/56. This fraction can be simplified by dividing both numerator and denominator by 7, resulting in 5/8.
-
Convert back to decimal: To express the answer as a decimal, divide 5 by 8, which yields 0.625.
Method 3: Calculator
The simplest method is using a calculator. Enter 3.5 ÷ 5.6 and the calculator will directly provide the answer: 0.625. While efficient, understanding the underlying principles is vital for problem-solving beyond simple calculations.
Significant Figures and Accuracy
The accuracy of the result is influenced by the significant figures in the original numbers (3.5 and 5.6). Both numbers have two significant figures. Therefore, the answer should ideally also be expressed with two significant figures. Rounding 0.625 to two significant figures gives 0.62. However, in this specific case, the answer is an exact decimal value, 0.625 which has three significant figures, but we could round it to 0.63 depending on the context and the desired level of precision.
Real-World Applications
Understanding division, particularly with decimals, is fundamental in many real-world scenarios:
- Finance: Calculating unit prices, interest rates, and proportions of investments.
- Engineering: Determining ratios, scaling measurements, and calculating material quantities.
- Science: Analyzing experimental data, converting units, and calculating concentrations.
- Cooking: Adjusting recipes and calculating ingredient proportions.
Extending the Concept: Division with More Complex Numbers
The principles demonstrated in solving 3.5 ÷ 5.6 extend to more complex division problems involving larger numbers, multiple decimal places, or even negative numbers. The core concepts remain the same: understanding the relationship between the dividend and divisor, employing appropriate calculation methods, and paying attention to the accuracy and precision of the result.
Troubleshooting Common Mistakes
Common mistakes in division problems often involve:
- Incorrect decimal placement: Misplacing the decimal point during long division can lead to significant errors.
- Errors in simplification: Mistakes in simplifying fractions can affect the accuracy of the final answer.
- Rounding errors: Inaccurate rounding can accumulate and distort the final result, especially in multi-step calculations.
Conclusion: Mastering Division for Enhanced Problem-Solving
Mastering division, particularly with decimals, is a cornerstone of mathematical literacy. Understanding the different methods – long division, fraction conversion, and calculator use – equips you with versatile tools for tackling various problems. Moreover, grasping the concept of significant figures ensures accuracy and precision in your results. The seemingly simple problem of 3.5 divided by 5.6, therefore, serves as a gateway to understanding broader mathematical concepts and their real-world applications. By mastering these concepts, you build a stronger foundation for tackling more complex mathematical challenges and for enhancing your problem-solving capabilities across diverse fields. Remember to always check your work and understand the context of the problem to ensure accurate and meaningful results. The seemingly mundane task of division holds a significant role in our capacity to comprehend and interact with the quantitative aspects of our world.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 90 And 135
May 24, 2025
-
What Is 35 4 As A Decimal
May 24, 2025
-
What Is 1 Divided By 2 3
May 24, 2025
-
What Is 40 Off Of 40 Dollars
May 24, 2025
-
How Many Seconds Are In 3 5 Hours
May 24, 2025
Related Post
Thank you for visiting our website which covers about 3 5 Divided By 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.