3/4 Of What Number Is 10
listenit
May 11, 2025 · 5 min read
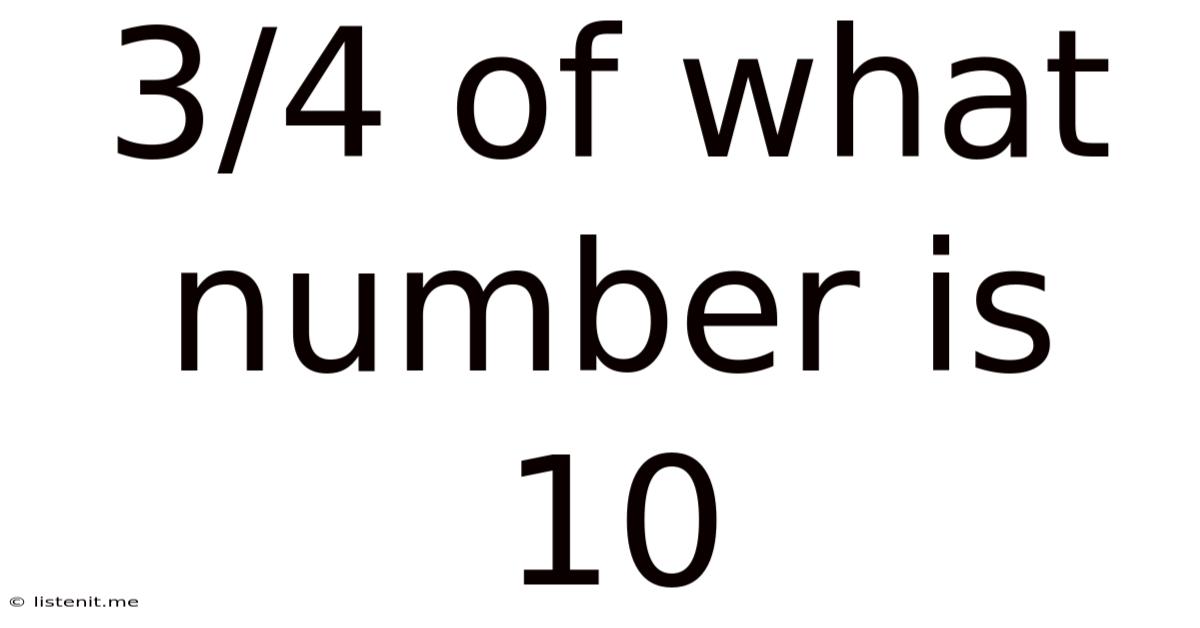
Table of Contents
3/4 of What Number is 10? Unlocking the Power of Proportions
This seemingly simple question, "3/4 of what number is 10?", opens the door to a fascinating exploration of mathematical proportions, problem-solving strategies, and real-world applications. While the answer itself is straightforward, understanding the underlying concepts and various methods to arrive at the solution enhances mathematical fluency and critical thinking skills. This article will delve into multiple approaches to solve this problem, emphasizing the importance of understanding the principles behind the calculations. We'll also explore how this type of problem translates into various practical scenarios.
Understanding the Problem: Deconstructing the Question
The core of the problem lies in interpreting the phrase "3/4 of what number is 10". This translates into a mathematical equation. We can represent the unknown number with a variable, typically 'x'. The phrase "3/4 of" indicates multiplication. Therefore, the complete equation becomes:
(3/4) * x = 10
This equation forms the basis for our problem-solving endeavors. We'll explore several methods to solve for 'x', highlighting the strengths and weaknesses of each approach.
Method 1: The Direct Algebraic Approach
This is the most straightforward method. To isolate 'x', we need to perform inverse operations. Since 'x' is multiplied by (3/4), we'll divide both sides of the equation by (3/4):
x = 10 / (3/4)
Remember that dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of (3/4) is (4/3). Therefore:
x = 10 * (4/3) = 40/3 = 13.333...
Therefore, 3/4 of 13.333... is approximately 10. The recurring decimal indicates that this is a rational number, not a whole number. This is perfectly acceptable; many real-world problems don't yield whole number solutions.
Understanding the Reciprocal: A Key Concept
The use of the reciprocal is crucial in this method. The reciprocal of a number is simply 1 divided by that number. Understanding reciprocals is fundamental in algebra, particularly when solving equations involving fractions.
Method 2: Using Cross-Multiplication (Proportions)
This method utilizes the concept of proportions. We can set up a proportion:
3/4 = 10/x
This reads as "3 is to 4 as 10 is to x". Cross-multiplication provides an elegant way to solve for x:
3 * x = 4 * 10
3x = 40
x = 40/3 = 13.333...
This method reinforces the understanding of proportional relationships, a vital concept in many fields, including scaling, geometry, and even cooking.
Proportions in Real Life: Scaling and Recipes
Understanding proportions is crucial in various everyday tasks. Think about scaling recipes – if a recipe calls for 2 cups of flour and 1 cup of sugar, and you want to double the recipe, you maintain the proportion by doubling both ingredients. Similarly, scaling maps and blueprints relies heavily on consistent proportions.
Method 3: The Percentage Approach
We can approach this problem using percentages. The fraction 3/4 represents 75% (3/4 * 100% = 75%). The problem can be restated as:
75% of what number is 10?
This can be written as:
0.75 * x = 10
Solving for x:
x = 10 / 0.75 = 13.333...
This method showcases the interconnectivity between fractions, decimals, and percentages – all essential elements of mathematical literacy.
Percentages in Daily Life: Discounts and Taxes
Percentages are ubiquitous in our daily lives. Calculating discounts, taxes, interest rates, and tips all rely on a strong understanding of percentages. Mastering this method improves financial literacy and everyday problem-solving skills.
Method 4: Visual Representation (Fractions on a Number Line)
While less algebraic, a visual approach can provide valuable intuition. Imagine a number line. If 3/4 of a number is 10, we can divide the number line into four equal parts. Three of these parts represent 10. Therefore, one part represents 10/3. The entire number (four parts) would be 4 * (10/3) = 40/3 = 13.333...
This method strengthens visual and spatial reasoning skills, beneficial for understanding mathematical concepts intuitively.
Visual Methods Enhance Understanding: Geometry and Data Visualization
Visual methods are incredibly powerful, particularly in geometry and data visualization. Graphs, charts, and diagrams provide alternative ways to represent and understand complex information, aiding comprehension and communication.
Real-World Applications: Beyond the Classroom
The seemingly simple equation "(3/4) * x = 10" has far-reaching implications in various real-world scenarios:
- Construction and Engineering: Calculating material quantities, adjusting blueprints, and determining scaling factors in construction projects often involve proportional reasoning.
- Finance and Budgeting: Calculating percentages of income, expenses, and interest rates requires proficiency in solving proportional equations.
- Data Analysis and Statistics: Understanding proportions and percentages is crucial for interpreting data, drawing inferences, and making informed decisions.
- Cooking and Baking: Scaling recipes, adjusting ingredient quantities, and understanding ratios are all based on proportional reasoning.
- Science and Research: Many scientific experiments and studies rely on the accurate calculation of proportions and ratios.
Conclusion: Mastering Proportions for a Brighter Future
The question "3/4 of what number is 10?" is more than just a simple mathematical problem. It's a gateway to understanding fundamental mathematical principles, including proportions, reciprocals, fractions, decimals, and percentages. Mastering these concepts not only enhances mathematical skills but also equips individuals with essential problem-solving abilities applicable across diverse fields. By exploring multiple approaches to solving this equation and understanding its real-world applications, we gain a deeper appreciation for the power and versatility of mathematics in our daily lives. Further exploration of these concepts will undoubtedly enhance mathematical fluency and foster a deeper understanding of the interconnectedness of various mathematical branches. The more we explore these seemingly simple equations, the more we unlock a vast world of possibilities.
Latest Posts
Latest Posts
-
What Is Half Of 3 And 1 3 Cups
May 12, 2025
-
Write The Complete Ground State Electron Configuration Of Chromium
May 12, 2025
-
What Is The Unit Used To Measure Weight
May 12, 2025
-
The Sum Of A Number And 15
May 12, 2025
-
Is An Inflection Point A Critical Point
May 12, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Of What Number Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.