3/4 Divided By 9/2 In Fraction
listenit
May 23, 2025 · 5 min read
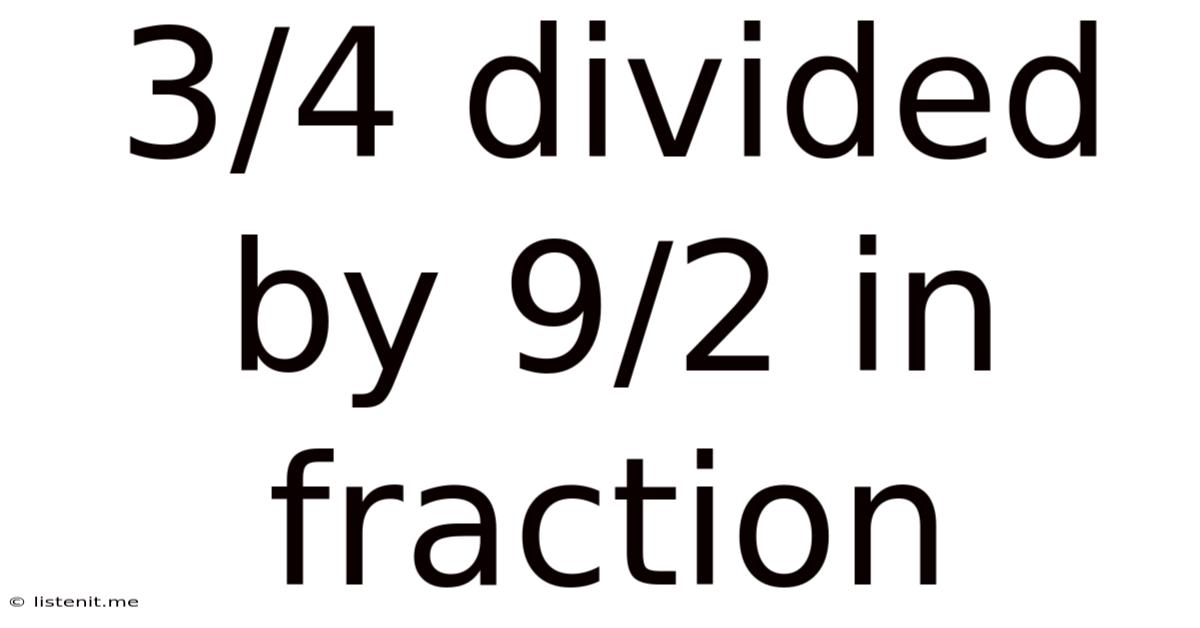
Table of Contents
3/4 Divided by 9/2 in Fraction: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 3/4 by 9/2, explaining the steps involved, providing alternative methods, and exploring related concepts to solidify your understanding of fraction division.
Understanding Fraction Division
Before diving into the specific problem, let's establish a firm grasp of the fundamental principles of dividing fractions. The core concept revolves around reciprocals and multiplication. Instead of directly dividing fractions, we transform the division problem into a multiplication problem by using the reciprocal of the second fraction (the divisor).
The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. The reciprocal of a whole number (like 5) is 1/5.
Therefore, the rule for dividing fractions is:
Fraction 1 ÷ Fraction 2 = Fraction 1 × Reciprocal of Fraction 2
Step-by-Step Solution: 3/4 ÷ 9/2
Now, let's apply this rule to our problem: 3/4 ÷ 9/2.
Step 1: Find the reciprocal of the second fraction.
The second fraction (divisor) is 9/2. Its reciprocal is 2/9.
Step 2: Rewrite the division as multiplication.
Our problem now becomes: 3/4 × 2/9
Step 3: Multiply the numerators (top numbers) together.
3 × 2 = 6
Step 4: Multiply the denominators (bottom numbers) together.
4 × 9 = 36
Step 5: Simplify the resulting fraction.
Our initial result is 6/36. We can simplify this fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 6 and 36 is 6. Dividing both the numerator and the denominator by 6, we get:
6 ÷ 6 = 1 36 ÷ 6 = 6
Therefore, the simplified answer is 1/6.
Alternative Methods and Visualizations
While the method above is the standard approach, visualizing the division of fractions can enhance understanding. Let's explore alternative methods.
Using a Visual Representation with Area Models
Imagine a rectangle representing the whole (1). We can divide this rectangle into four equal parts to represent 3/4. Now, we need to divide these 3/4 into pieces of size 9/2. This might seem difficult visually, but the key is to remember that we're looking for how many 9/2 "pieces" fit into 3/4. This visual representation helps solidify the concept of division as finding "how many times" one fraction fits into another. The area model demonstrates that 1/6 of the whole would be the appropriate size.
Converting to Improper Fractions and Decimals (Less Efficient but Illustrative)
While not the most efficient method for this specific problem, converting fractions to decimals can offer another perspective.
First, convert 3/4 to a decimal: 3 ÷ 4 = 0.75
Next, convert 9/2 to a decimal: 9 ÷ 2 = 4.5
Now, divide 0.75 by 4.5: 0.75 ÷ 4.5 = 0.1666... (This is approximately 1/6)
Although this method yields the correct answer, it’s often less efficient and can introduce rounding errors. It’s crucial to retain the fraction form for accuracy, especially in more complex fraction calculations.
Expanding on Fraction Division Concepts
Understanding fraction division extends beyond the solution to a single problem. Let's explore some related concepts that deepen your grasp of this essential mathematical skill.
Dividing by Fractions Less Than One
When dividing by a fraction less than one (like 9/2 in our problem), the result will be larger than the original fraction. This is because you're essentially asking, "How many times does a small fraction fit into a larger fraction?" The answer will always be greater than 1.
Dividing by Fractions Greater Than One
Conversely, if you divide a fraction by a fraction greater than one, the result will be smaller than the original fraction. This is intuitive: you're asking how many times a large fraction fits into a smaller one; the answer must be less than one.
Complex Fractions
A complex fraction has a fraction in the numerator, the denominator, or both. For example, (3/4) / (9/2) is a complex fraction. The method of converting the division to multiplication using the reciprocal applies equally well to complex fractions.
Mixed Numbers and Fraction Division
When dealing with mixed numbers (like 1 ½), convert them to improper fractions before performing the division. For instance, 1 ½ is equivalent to 3/2. Then, apply the standard fraction division steps.
Real-World Applications of Fraction Division
Fraction division is essential in various real-world scenarios:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions.
- Sewing and Crafts: Calculating fabric needs or other material quantities involves dividing fractions.
- Construction and Engineering: Dividing fractions is vital for precise measurements and calculations.
- Data Analysis: When working with proportions and percentages, fraction division is a common tool.
Troubleshooting Common Mistakes
Several common mistakes can occur when dividing fractions. Here are some to watch out for:
- Forgetting to find the reciprocal: Remember to flip the second fraction before multiplying.
- Incorrect multiplication: Double-check your multiplication of numerators and denominators.
- Failing to simplify: Always simplify the resulting fraction to its lowest terms.
- Improper conversion of mixed numbers: Ensure you accurately convert mixed numbers to improper fractions before proceeding.
Conclusion
Dividing 3/4 by 9/2 results in 1/6. This guide has explored this specific problem in detail, providing a step-by-step solution, alternative methods, and expanded on related concepts to solidify your understanding. Mastering fraction division is a crucial skill that extends to various areas of mathematics and real-world applications. Remember to practice regularly, focusing on each step, to build confidence and accuracy. By understanding the underlying principles, you can tackle any fraction division problem with ease.
Latest Posts
Latest Posts
-
What Year Are 17 Year Olds Born
May 24, 2025
-
The Area To The Left Of Z
May 24, 2025
-
How Fast Is 52 Km In Mph
May 24, 2025
-
3 30 To 5 30 Is How Many Hours
May 24, 2025
-
5 Is What Percent Of 16
May 24, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Divided By 9/2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.