3 4 Divided By 5 6
listenit
May 25, 2025 · 5 min read
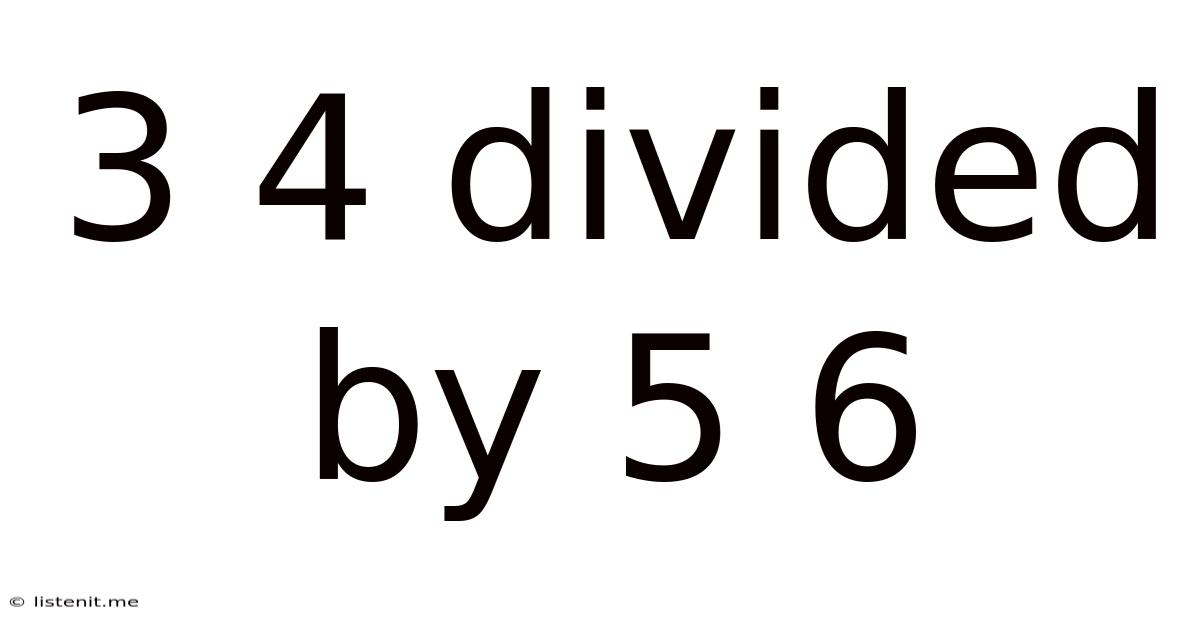
Table of Contents
Decoding the Mystery: 3/4 Divided by 5/6 – A Deep Dive into Fraction Division
The seemingly simple problem of dividing fractions, like 3/4 divided by 5/6, often trips up students and even adults. It's more than just a rote calculation; it represents a fundamental concept in mathematics with broad applications. This comprehensive guide will explore this specific problem, breaking down the process step-by-step and explaining the underlying principles that govern fraction division. We'll delve into various approaches, highlight practical examples, and even touch upon advanced concepts for a truly thorough understanding.
Understanding the Basics: What Does Fraction Division Mean?
Before tackling 3/4 ÷ 5/6, let's solidify our understanding of fraction division. When we divide one fraction by another, we're essentially asking: "How many times does the second fraction fit into the first?" This question is key to visualizing and comprehending the operation.
Imagine you have a pizza cut into four slices (3/4 of the pizza). You want to share this portion equally among groups, where each group receives 5/6 of a pizza. The division 3/4 ÷ 5/6 answers the question: How many of these 5/6 pizza-sized groups can you create from your 3/4 slice?
Method 1: The "Keep, Change, Flip" Method
This popular method provides a simple, algorithmic approach to fraction division. It's memorable and effective, but understanding why it works is crucial for true mathematical literacy.
The Steps:
- Keep: Keep the first fraction (the dividend) exactly as it is: 3/4.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (the divisor) – this is called finding the reciprocal. The reciprocal of 5/6 is 6/5.
Now, we have a multiplication problem: 3/4 × 6/5.
- Multiply: Multiply the numerators (top numbers) together: 3 × 6 = 18.
- Multiply: Multiply the denominators (bottom numbers) together: 4 × 5 = 20.
This gives us the result: 18/20.
- Simplify: We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 2. This simplifies to 9/10.
Therefore, 3/4 divided by 5/6 equals 9/10.
Method 2: Understanding the Reciprocal
The "Keep, Change, Flip" method is a shortcut for a more fundamental principle: dividing by a fraction is the same as multiplying by its reciprocal. A reciprocal is simply the fraction flipped upside down.
Why does this work? Let's consider a simpler example: 1 ÷ (1/2). This means: How many halves are in one whole? The answer is two. Multiplying 1 by the reciprocal of 1/2 (which is 2/1 or 2) gives us the same result: 1 × 2 = 2.
Applying this principle to our problem:
3/4 ÷ 5/6 = 3/4 × 6/5 = 18/20 = 9/10.
Method 3: Using Complex Fractions
Another way to approach this problem is through complex fractions. A complex fraction is a fraction where the numerator or denominator (or both) contains a fraction. We can represent the division problem as a complex fraction:
(3/4) / (5/6)
To simplify a complex fraction, we multiply both the numerator and the denominator by the reciprocal of the denominator:
[(3/4) × (6/5)] / [(5/6) × (6/5)]
This simplifies to:
(18/20) / 1 = 18/20 = 9/10
Practical Applications: Real-World Scenarios
Fraction division isn't confined to the classroom; it's frequently used in various real-world situations:
-
Baking: If a recipe calls for 3/4 cup of flour, but you only want to make 5/6 of the recipe, how much flour do you need? (3/4) × (5/6) = 15/24 = 5/8 cup. (This is a multiplication problem, not division. Note the difference in the problem type).
-
Construction: If a wall requires 5/6 of a sheet of drywall, and you have 3/4 of a sheet, how many walls can you partially complete? (3/4) ÷ (5/6) = 9/10. You can complete 9/10 of a wall.
-
Sewing: If a pattern calls for 5/6 of a yard of fabric, and you have 3/4 of a yard, will you have enough? This requires the same calculation as above; you have less than you need.
Advanced Concepts and Extensions
While 3/4 ÷ 5/6 demonstrates basic fraction division, the principles extend to more complex scenarios:
-
Dividing Mixed Numbers: Mixed numbers (like 1 1/2) need to be converted to improper fractions before applying the division methods outlined above.
-
Dividing Fractions with Variables: The same principles apply when fractions contain variables (algebra).
-
Decimal Equivalents: Converting fractions to decimals can sometimes simplify the calculation, especially with the aid of a calculator, but understanding the fractional representation remains essential for grasping the underlying mathematical concepts.
Conclusion: Mastering Fraction Division
Mastering fraction division, as illustrated through the example of 3/4 ÷ 5/6, is crucial for building a strong foundation in mathematics. While the "Keep, Change, Flip" method provides a convenient shortcut, understanding the underlying principle of multiplying by the reciprocal enhances your mathematical understanding and prepares you for more advanced concepts. By exploring various approaches and applying the concepts to practical examples, you can confidently tackle similar problems and confidently use fraction division in real-world situations. Remember, consistent practice is key to mastering this fundamental mathematical operation. Don't just memorize the steps; strive to understand the why behind the method. This deeper understanding will empower you to solve more complex problems with greater ease and confidence.
Latest Posts
Latest Posts
-
What Size Ac Unit For 700 Sq Ft
May 25, 2025
-
Greatest Common Factor Of 12 And 44
May 25, 2025
-
What Is 30 Percent Of 140
May 25, 2025
-
3 To 1 Mix Ratio Calculator
May 25, 2025
-
4 Divided By 9 2 In Fraction Form
May 25, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.