3/4 Divided By 12 As A Fraction
listenit
May 25, 2025 · 5 min read
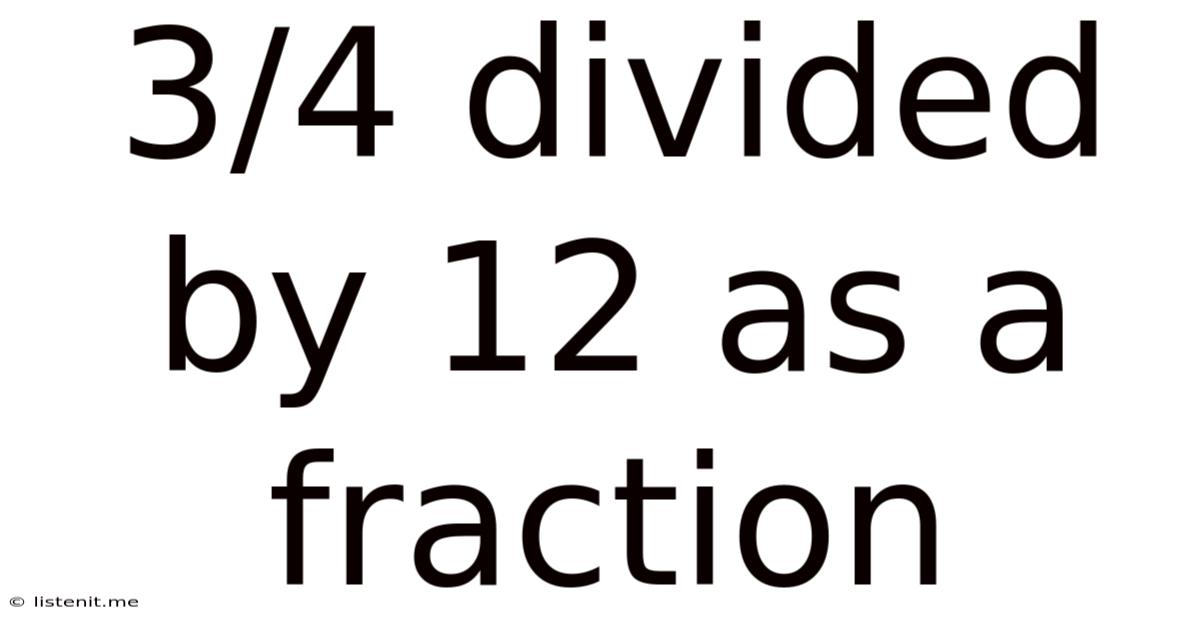
Table of Contents
3/4 Divided by 12 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing the fraction 3/4 by 12, explaining the steps in detail and providing context for similar problems. We'll explore different approaches, emphasizing the importance of understanding the underlying mathematical principles. This will not only help you solve this specific problem but also equip you with the skills to tackle a wide range of fraction division problems.
Understanding Fraction Division
Before diving into the specific problem of 3/4 divided by 12, let's solidify our understanding of fraction division. The core concept revolves around reciprocals and multiplication. When you divide a fraction by a whole number (or another fraction), you are essentially multiplying the first fraction by the reciprocal of the second.
The reciprocal of a number is simply its multiplicative inverse. For example, the reciprocal of 2 is 1/2, because 2 * (1/2) = 1. The reciprocal of 3/4 is 4/3. This is crucial because dividing by a number is equivalent to multiplying by its reciprocal.
Therefore, the rule for dividing fractions is:
To divide a fraction by a number, multiply the fraction by the reciprocal of that number.
Solving 3/4 Divided by 12
Now, let's apply this rule to our problem: 3/4 divided by 12.
First, we need to express 12 as a fraction: 12/1. This doesn't change its value; it simply represents the whole number as a fraction.
Next, we find the reciprocal of 12/1, which is 1/12.
Finally, we multiply 3/4 by 1/12:
(3/4) ÷ (12/1) = (3/4) x (1/12)
To multiply fractions, we multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(3 x 1) / (4 x 12) = 3/48
Now, we simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 3 and 48 is 3. Dividing both the numerator and denominator by 3, we get:
3/48 = 1/16
Therefore, 3/4 divided by 12 is equal to 1/16.
Alternative Approaches and Visualizations
While the reciprocal method is the most efficient, understanding alternative approaches can enhance your comprehension of fraction division.
Visual Representation
Imagine you have a pizza cut into four slices (representing 3/4). You want to divide these three slices among 12 people. Each person would get a tiny portion, which is 1/16th of the whole pizza. This visual representation helps to ground the abstract mathematical concept in a tangible scenario.
Step-by-Step Breakdown with Keywords for SEO:
Here's a step-by-step breakdown, incorporating relevant keywords for improved search engine optimization:
-
Identify the Dividend and Divisor: In the problem "3/4 divided by 12," 3/4 is the dividend, and 12 is the divisor. Understanding these terms is fundamental in fraction division.
-
Convert the Whole Number to a Fraction: Express the whole number divisor (12) as a fraction: 12/1. This step is crucial for applying the fraction division rule.
-
Find the Reciprocal: The reciprocal of 12/1 is 1/12. Finding the reciprocal is a key step in the process of dividing fractions.
-
Multiply the Fractions: Multiply the dividend (3/4) by the reciprocal of the divisor (1/12): (3/4) * (1/12) = 3/48. This multiplication step utilizes the fundamental rule of fraction division.
-
Simplify the Result: Simplify the resulting fraction (3/48) by finding the greatest common factor (GCF) of the numerator and the denominator, which is 3. Dividing both numerator and denominator by 3 results in the simplified fraction 1/16. This step involves fraction simplification, a crucial aspect of mathematical accuracy.
Expanding on Fraction Division Concepts
Understanding the problem of 3/4 divided by 12 is a stepping stone to mastering more complex fraction division problems. Let's explore some related concepts:
Dividing Fractions by Fractions
The same principle applies when dividing a fraction by another fraction. For example, let's consider (1/2) ÷ (2/3):
-
Find the reciprocal of the divisor (2/3), which is (3/2).
-
Multiply the dividend (1/2) by the reciprocal: (1/2) * (3/2) = 3/4
Therefore, (1/2) ÷ (2/3) = 3/4.
Mixed Numbers and Fraction Division
When dealing with mixed numbers, the first step is to convert them into improper fractions before applying the division rule. For example, to divide 1 1/2 by 2/3:
-
Convert 1 1/2 to an improper fraction: (3/2)
-
Find the reciprocal of 2/3: (3/2)
-
Multiply: (3/2) * (3/2) = 9/4 or 2 1/4
Therefore, 1 1/2 ÷ (2/3) = 9/4 or 2 1/4
Real-World Applications of Fraction Division
Fraction division isn't just a theoretical exercise. It has numerous real-world applications across various fields:
-
Cooking and Baking: Scaling recipes up or down often involves dividing fractions. For example, if a recipe calls for 1/2 cup of flour and you want to make only half the recipe, you would need to divide 1/2 by 2.
-
Construction and Engineering: Precise measurements in construction and engineering frequently involve fractions and their division.
-
Finance: Calculating portions of shares or splitting financial assets might involve dividing fractions.
-
Science: Many scientific calculations, particularly in chemistry and physics, require the division of fractions.
Conclusion: Mastering Fraction Division
Mastering fraction division, as demonstrated by solving 3/4 divided by 12, is crucial for success in mathematics and its various applications. Remember the key steps: convert whole numbers to fractions, find the reciprocal, multiply, and simplify. By understanding the underlying principles and practicing regularly, you can confidently tackle any fraction division problem. This comprehensive guide has equipped you not only with the solution to the specific problem but also with a solid foundation to tackle future fraction-related challenges. Remember to practice regularly and utilize different approaches to strengthen your understanding. The more you practice, the easier it becomes.
Latest Posts
Latest Posts
-
How To Construct A 90 Confidence Interval
May 25, 2025
-
How Long Is 8 Months In Days
May 25, 2025
-
What Is The Least Common Multiple Of 8 And 18
May 25, 2025
-
39 Divided By 4641 As A Fraction
May 25, 2025
-
31 What Year Was I Born
May 25, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Divided By 12 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.