3 4 And 3 4 Equals
listenit
May 25, 2025 · 6 min read
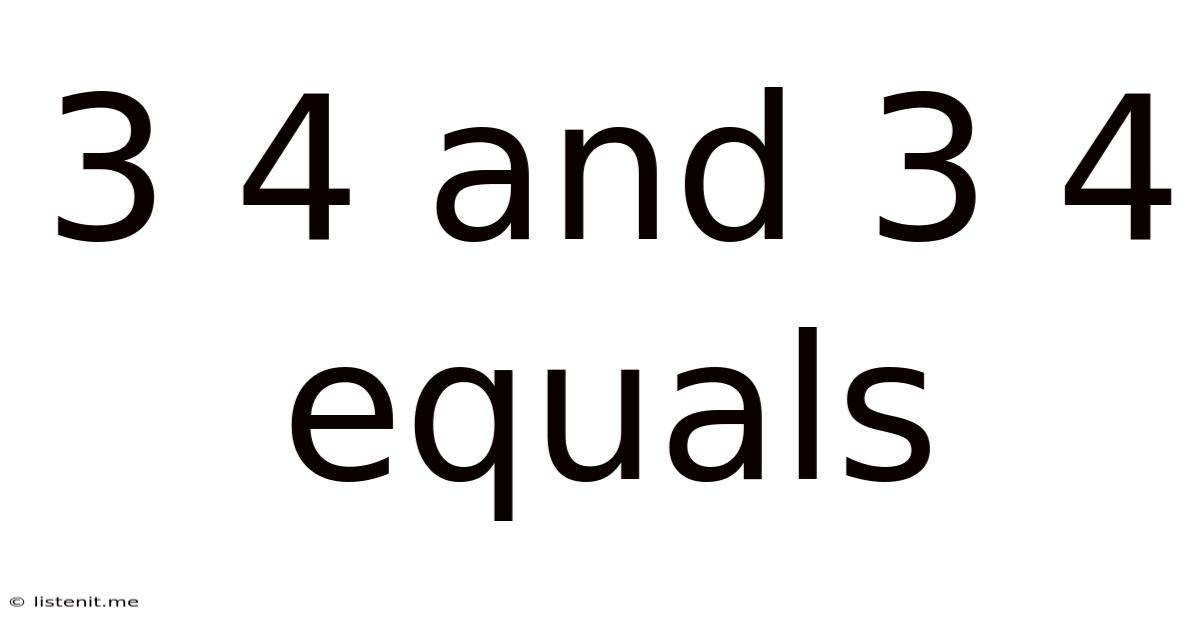
Table of Contents
Decoding 3/4 + 3/4: A Deep Dive into Fractions and Their Applications
The seemingly simple equation, 3/4 + 3/4, often presents a stumbling block for many, particularly those lacking a strong foundation in fractions. However, understanding this seemingly basic calculation unlocks a broader understanding of fractional arithmetic, its applications in various fields, and the importance of mastering this fundamental concept. This article will explore the solution to 3/4 + 3/4, delve into the underlying principles of fraction addition, and showcase the practical relevance of this knowledge in everyday life and specialized fields.
Understanding Fractions: A Quick Refresher
Before tackling the equation, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In the equation 3/4 + 3/4, both fractions share a common denominator of 4. This means both fractions represent parts of a whole that has been divided into four equal sections. The numerator, 3, indicates that we have three of those four parts in each fraction.
Adding Fractions with a Common Denominator
The beauty of adding fractions with a common denominator lies in its simplicity. Since the denominators are the same, we are essentially adding parts of the same size. Therefore, we only need to add the numerators while keeping the denominator consistent.
The Process:
-
Check the denominators: Ensure both fractions have the same denominator. In this case, both fractions have a denominator of 4.
-
Add the numerators: Add the numerators together: 3 + 3 = 6
-
Keep the denominator the same: The denominator remains 4.
-
Result: The sum is 6/4.
Therefore, 3/4 + 3/4 = 6/4.
Simplifying Fractions: Reducing to Lowest Terms
The fraction 6/4, while correct, can be simplified. Simplifying, or reducing to lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1.
The Process:
-
Find the greatest common divisor (GCD): The GCD of 6 and 4 is 2. This means both numbers are divisible by 2.
-
Divide both the numerator and denominator by the GCD: 6 divided by 2 is 3, and 4 divided by 2 is 2.
-
Simplified fraction: The simplified fraction is 3/2.
Therefore, 6/4 simplifies to 3/2.
Converting to Mixed Numbers: Representing the Whole and Part
The fraction 3/2 is an improper fraction because the numerator (3) is larger than the denominator (2). Improper fractions can be converted into mixed numbers, which represent a combination of a whole number and a proper fraction.
The Process:
-
Divide the numerator by the denominator: 3 divided by 2 is 1 with a remainder of 1.
-
The whole number: The quotient (1) becomes the whole number part of the mixed number.
-
The fraction: The remainder (1) becomes the numerator of the fraction, and the denominator remains the same (2).
-
Mixed number: The mixed number is 1 1/2.
Therefore, 3/2 is equivalent to 1 1/2.
Final Answer and Conclusion: 3/4 + 3/4 = 1 1/2
In summary, after adding the fractions, simplifying, and converting to a mixed number, we arrive at the final answer:
3/4 + 3/4 = 1 1/2
This seemingly simple equation provides a foundational understanding of fraction addition, simplification, and conversion. Mastering these steps is crucial for tackling more complex mathematical problems.
Real-World Applications of Fraction Addition
The principles involved in adding 3/4 and 3/4 extend far beyond the classroom. Fractions are ubiquitous in everyday life and professional fields:
1. Cooking and Baking: Recipes frequently call for fractional measurements. Adding ingredients involves precisely calculating fractions. For example, a recipe might require 3/4 cup of sugar and another 3/4 cup of flour, requiring you to add these fractions to determine the total amount of dry ingredients.
2. Construction and Engineering: Precise measurements are paramount in construction and engineering. Engineers and architects regularly use fractions to plan layouts, calculate materials needed, and ensure accuracy in construction projects. Calculating the length of materials requires using fractions effectively, and this process is similar to adding 3/4 + 3/4.
3. Finance and Budgeting: Managing personal finances necessitates understanding fractions and decimals. Calculating percentages, discounts, or proportions of your monthly budget relies on fractional arithmetic skills.
4. Data Analysis and Statistics: Fractions are integral to statistics. Data analysis often involves dealing with proportions, percentages, and probabilities, all based on the underlying principles of fractions.
5. Science and Medicine: In fields like chemistry, physics, and medicine, precise measurements are critical. Dealing with concentrations, dosages, or volumes often relies heavily on fractional calculations. Imagine needing to determine the total dosage of medication that is given in 3/4 ml increments over several doses.
Beyond the Basics: Adding Fractions with Unlike Denominators
While the equation 3/4 + 3/4 involves fractions with common denominators, more complex fraction addition may involve fractions with unlike denominators. In such cases, the first step is finding a common denominator before adding the numerators. This typically involves finding the least common multiple (LCM) of the denominators. For instance, consider the addition of 1/2 + 1/3:
-
Find the LCM: The LCM of 2 and 3 is 6.
-
Convert fractions to have a common denominator: 1/2 becomes 3/6 (multiplying both numerator and denominator by 3), and 1/3 becomes 2/6 (multiplying both numerator and denominator by 2).
-
Add the numerators: 3/6 + 2/6 = 5/6
Therefore, 1/2 + 1/3 = 5/6.
This demonstrates the importance of understanding the fundamentals of fraction addition, as it forms the basis for solving more complex problems.
Advanced Applications: Fractions in Calculus and Beyond
The seemingly simple concepts of adding fractions extend far beyond basic arithmetic. In higher-level mathematics like calculus, fractions are used extensively. Derivatives and integrals often involve manipulating and simplifying complex fractional expressions. Understanding the basic principles of adding fractions is thus a crucial stepping stone towards more advanced mathematical concepts.
Mastering Fractions: A Path to Mathematical Proficiency
The ability to confidently add fractions, such as 3/4 + 3/4, is not merely about getting the correct answer. It signifies a grasp of foundational mathematical concepts that underpin numerous other areas of study and practical applications. From understanding recipes to managing budgets, calculating dosages to interpreting data, the ability to manipulate fractions fluently is an invaluable skill applicable across a vast spectrum of disciplines. Consistent practice and a thorough understanding of the underlying principles are key to achieving mathematical proficiency and unlocking the full potential of fractional arithmetic. The more comfortable you become with these basics, the easier it will be to tackle more complex mathematical challenges in the future. Therefore, invest the time to truly understand this fundamental concept, and you will reap the rewards in your academic pursuits and in your everyday life.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 5 6 7
May 25, 2025
-
B Cup Breast Size In Cm
May 25, 2025
-
How To Calculate Stair Square Footage
May 25, 2025
-
How To Figure Weight Of Concrete
May 25, 2025
-
2 Hour 22 Minute Marathon Pace
May 25, 2025
Related Post
Thank you for visiting our website which covers about 3 4 And 3 4 Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.