3/4 + 1/2 Answer In Fraction
listenit
May 09, 2025 · 5 min read
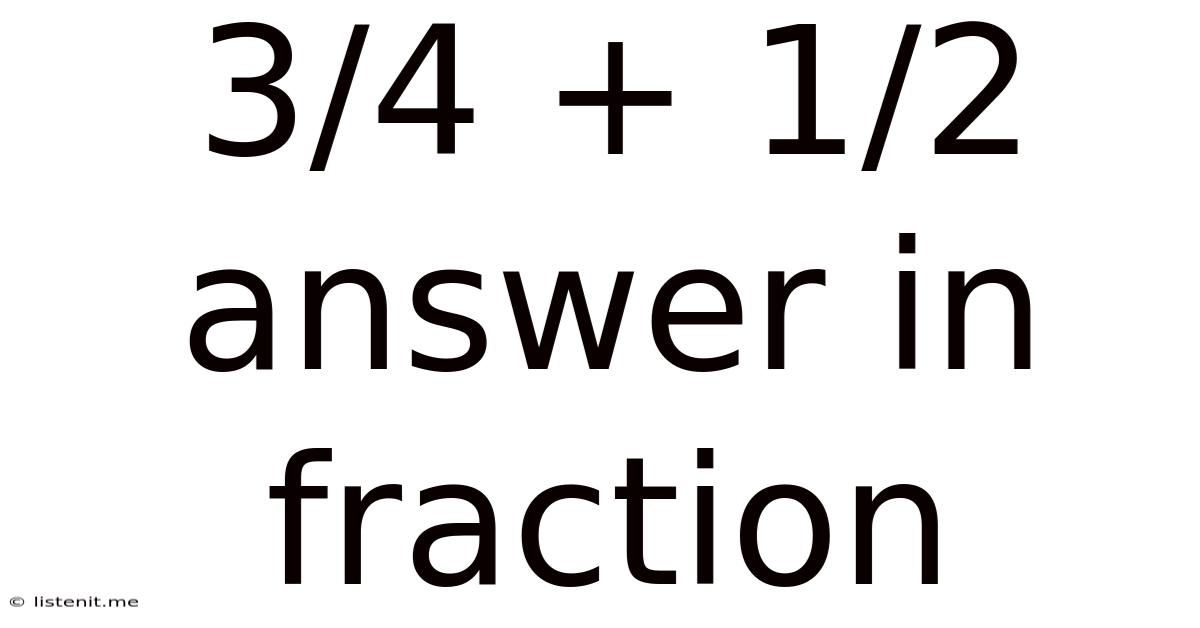
Table of Contents
3/4 + 1/2: A Deep Dive into Fraction Addition and its Applications
Adding fractions might seem like a simple arithmetic task, but a solid understanding of the underlying principles is crucial for success in higher-level mathematics and various real-world applications. This article delves into the process of adding 3/4 and 1/2, explaining the steps involved, exploring the underlying concepts, and showcasing practical examples where this type of calculation is essential. We'll also explore some common mistakes and offer tips to avoid them.
Understanding Fractions
Before we tackle the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator is 3 (we have 3 parts), and the denominator is 4 (the whole is divided into 4 equal parts).
Adding Fractions with Unlike Denominators
The core challenge in adding 3/4 and 1/2 lies in their unlike denominators. You cannot directly add fractions unless they share a common denominator. This is because you're adding parts of different sizes. Imagine trying to add three quarters of a pizza to half a pizza – you need to express them in terms of the same size slice before you can combine them.
To find a common denominator, we look for the least common multiple (LCM) of the denominators 4 and 2. The LCM is the smallest number that both 4 and 2 divide into evenly. In this case, the LCM of 4 and 2 is 4.
Converting Fractions to a Common Denominator
Now, we need to convert both fractions to have a denominator of 4:
-
3/4 already has a denominator of 4, so it remains unchanged.
-
1/2 needs to be converted. To achieve a denominator of 4, we multiply both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4. This is crucial because multiplying both the numerator and denominator by the same number doesn't change the value of the fraction; it simply changes its representation.
Adding the Fractions
Now that both fractions have a common denominator of 4, we can add them:
3/4 + 2/4 = (3 + 2) / 4 = 5/4
Simplifying the Result
The result, 5/4, is an improper fraction (the numerator is larger than the denominator). We can simplify this into a mixed number, which combines a whole number and a fraction. To do this, we divide the numerator (5) by the denominator (4):
5 ÷ 4 = 1 with a remainder of 1.
This means that 5/4 is equal to 1 whole and 1/4. Therefore:
3/4 + 1/2 = 5/4 = 1 1/4
Visual Representation
Imagine two pizzas cut into four slices each. 3/4 of the first pizza represents three slices, and 1/2 of the second pizza represents two slices. When you combine these, you have a total of five slices, which is one whole pizza and one quarter of a pizza remaining. This visually confirms our calculation.
Real-World Applications
Understanding fraction addition is essential in numerous real-world scenarios, including:
Cooking and Baking:
Recipes frequently involve fractions. Adding ingredients, adjusting serving sizes, or understanding ratios all require accurate fraction addition. For instance, a recipe might require 1/2 cup of sugar and 3/4 cup of flour. Knowing how to add these fractions ensures you use the correct amounts.
Construction and Engineering:
Precise measurements are vital in construction and engineering projects. Workers may need to add fractional lengths of materials, calculate angles, or determine volumes. Accurate fraction addition ensures the project's structural integrity and functionality.
Finance and Budgeting:
Fractions are frequently used in financial calculations. Understanding fractional shares of stock, calculating interest rates, or managing portions of a budget requires accurate fraction arithmetic.
Data Analysis and Statistics:
Fraction addition is vital in interpreting data and performing statistical calculations. For example, calculating proportions of a population, expressing probabilities, or analyzing data sets may involve adding and manipulating fractions.
Common Mistakes to Avoid
Several common mistakes can hinder accurate fraction addition:
-
Adding numerators and denominators directly: This is incorrect. Remember, you must find a common denominator first.
-
Forgetting to simplify: Always simplify your answer to its lowest terms to ensure a concise and accurate result.
-
Incorrectly converting to a mixed number: Double-check your division when converting improper fractions into mixed numbers.
Advanced Concepts and Extensions
The addition of 3/4 and 1/2 provides a foundation for more complex fraction operations:
-
Subtraction of fractions: Similar principles apply to subtracting fractions. You'll still need to find a common denominator before performing the subtraction.
-
Multiplication and division of fractions: These operations involve different procedures compared to addition and subtraction.
-
Working with mixed numbers: Adding, subtracting, multiplying, and dividing mixed numbers often requires converting them into improper fractions first, then applying the relevant operation.
Conclusion
Adding fractions like 3/4 and 1/2 may seem straightforward, but mastering the process builds a solid foundation for more advanced mathematical concepts. Understanding the underlying principles, practicing regularly, and avoiding common mistakes will ensure accuracy and confidence in performing these calculations. The applications of fraction addition extend far beyond the classroom, making it a crucial skill for numerous real-world scenarios. By understanding the mechanics and developing proficiency in fraction arithmetic, you'll equip yourself with a valuable tool for problem-solving across many disciplines. Remember to always check your work and strive for accuracy and clarity in your calculations.
Latest Posts
Latest Posts
-
N Has How Many Valence Electrons
May 09, 2025
-
Why Environmental Science Is An Interdisciplinary Science
May 09, 2025
-
What Did Rutherford Expect To Happen In His Experiment
May 09, 2025
-
What Is One Fifth In Decimal Form
May 09, 2025
-
Eight More Than Twice A Number Is Eight
May 09, 2025
Related Post
Thank you for visiting our website which covers about 3/4 + 1/2 Answer In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.