3 2/5 As An Improper Fraction
listenit
Apr 07, 2025 · 6 min read
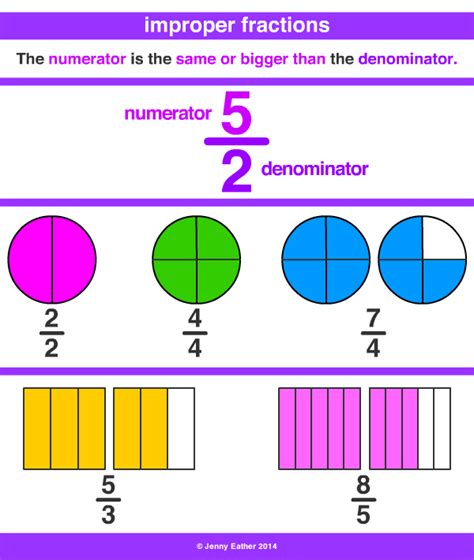
Table of Contents
3 2/5 as an Improper Fraction: A Comprehensive Guide
Understanding how to convert mixed numbers, like 3 2/5, into improper fractions is a fundamental skill in mathematics. This seemingly simple conversion forms the bedrock for more advanced mathematical operations, including multiplication and division of fractions. This comprehensive guide will not only show you how to convert 3 2/5 into an improper fraction but also delve into the why, providing a solid understanding of the underlying principles and offering various practical applications. We'll explore different methods, tackle common misconceptions, and offer tips and tricks to master this crucial skill.
What is a Mixed Number?
Before we dive into the conversion process, let's define our terms. A mixed number is a combination of a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). In our example, 3 2/5, '3' is the whole number and '2/5' is the proper fraction.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Improper fractions represent values greater than or equal to one. Converting mixed numbers to improper fractions allows us to represent these values in a single fractional unit, simplifying calculations.
Converting 3 2/5 to an Improper Fraction: Step-by-Step Guide
There are two main methods for converting a mixed number to an improper fraction. Let's explore both:
Method 1: The Multiplication and Addition Method
This method is generally considered the most efficient and straightforward:
-
Multiply the whole number by the denominator: In our case, multiply 3 (the whole number) by 5 (the denominator). This gives us 15.
-
Add the numerator: Add the result from step 1 (15) to the numerator of the fraction (2). This gives us 17.
-
Keep the same denominator: The denominator remains unchanged. It stays as 5.
-
Write the improper fraction: The result is 17/5. This is the improper fraction equivalent of 3 2/5.
Method 2: Visual Representation with Circles
This method is particularly helpful for visualizing the concept and is ideal for beginners.
Imagine three whole circles divided into fifths, plus an additional two-fifths of a circle.
-
Divide the whole circles: Each of the three whole circles can be divided into five equal parts (fifths).
-
Count the total fifths: Each whole circle contributes five fifths (5/5), giving a total of 15 fifths (3 x 5/5 = 15/5) from the three whole circles.
-
Add the remaining fraction: Add the two-fifths (2/5) from the additional part of the circle.
-
Total fifths: This gives us a total of 17 fifths (15/5 + 2/5 = 17/5). Thus, 3 2/5 is equivalent to 17/5.
Why Convert to Improper Fractions?
Converting mixed numbers to improper fractions is crucial for several reasons:
-
Simplifying Calculations: Many mathematical operations, especially multiplication and division of fractions, are significantly easier with improper fractions. Working directly with mixed numbers often requires multiple steps and can be more prone to errors.
-
Consistency: Using improper fractions provides a consistent format for all fractional values, whether they are greater than, equal to, or less than one. This consistency streamlines calculations and improves accuracy.
-
Advanced Math: Improper fractions are essential in more advanced mathematical concepts like algebra, calculus, and other areas of higher mathematics. A firm grasp of this conversion is a cornerstone for future learning.
Common Mistakes to Avoid
While the conversion process is relatively straightforward, some common mistakes can hinder accuracy:
-
Incorrect Multiplication: Ensure you correctly multiply the whole number by the denominator before adding the numerator. A simple multiplication error can lead to an incorrect improper fraction.
-
Forgetting the Denominator: Remember that the denominator remains unchanged throughout the conversion process. Keeping the denominator consistent is vital for the accuracy of your final answer.
-
Confusing Numerator and Denominator: Always double-check that you are adding the numerator to the product of the whole number and denominator, not vice versa.
Practical Applications of Improper Fractions
Improper fractions aren't just abstract mathematical concepts; they have numerous practical applications in everyday life and various fields:
-
Cooking and Baking: Recipes often require fractional measurements. Converting mixed numbers to improper fractions can simplify calculations, especially when scaling recipes up or down.
-
Construction and Engineering: Accurate measurements are critical in these fields. Converting to improper fractions can ensure precise calculations for dimensions and materials.
-
Financial Calculations: Dealing with fractions of money is commonplace in financial transactions. Converting mixed numbers to improper fractions can streamline calculations involving percentages, interest rates, and shares.
-
Data Analysis: In statistics and data analysis, improper fractions can simplify calculations involving proportions and ratios.
-
Sewing and Crafting: Precise measurements are important in these creative fields. Converting to improper fractions helps ensure accuracy in patterns and designs.
Beyond 3 2/5: Applying the Method to Other Mixed Numbers
The methods described above can be applied universally to convert any mixed number to its equivalent improper fraction. Let's try a few examples:
-
Convert 2 1/3 to an improper fraction:
- Multiply 2 (whole number) by 3 (denominator): 2 * 3 = 6
- Add the numerator: 6 + 1 = 7
- Keep the same denominator: 3
- Improper fraction: 7/3
-
Convert 5 3/4 to an improper fraction:
- Multiply 5 (whole number) by 4 (denominator): 5 * 4 = 20
- Add the numerator: 20 + 3 = 23
- Keep the same denominator: 4
- Improper fraction: 23/4
-
Convert 1 7/8 to an improper fraction:
- Multiply 1 (whole number) by 8 (denominator): 1 * 8 = 8
- Add the numerator: 8 + 7 = 15
- Keep the same denominator: 8
- Improper fraction: 15/8
These examples demonstrate the broad applicability of the conversion methods. Practice with various mixed numbers will solidify your understanding and improve your proficiency.
Mastering Improper Fractions: Tips and Tricks
-
Practice Regularly: Consistent practice is key to mastering any mathematical skill. Work through various examples, starting with simple mixed numbers and gradually progressing to more complex ones.
-
Visual Aids: Use visual aids like diagrams or manipulatives, especially when starting. These can help to visualize the conversion process and enhance understanding.
-
Check Your Work: Always double-check your calculations to ensure accuracy. A small error in multiplication or addition can lead to an incorrect result.
-
Utilize Online Resources: Numerous online resources and calculators can help you practice and verify your answers.
By understanding the principles behind the conversion of mixed numbers to improper fractions and practicing regularly, you'll gain confidence and proficiency in this essential mathematical skill. Remember, the ability to smoothly convert between mixed numbers and improper fractions is crucial for success in various mathematical endeavors and practical applications. Mastering this skill is a valuable asset that will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
Does A Trapezoid Have 4 Right Angles
Apr 08, 2025
-
The Central Part Of An Atom Containing Protons And Neutrons
Apr 08, 2025
-
Position The Following Items In Order Of Decreasing Size
Apr 08, 2025
-
Whats The Square Root Of 108
Apr 08, 2025
-
What Are The Two Most Common Elements In Earths Crust
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about 3 2/5 As An Improper Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.