3.125 As A Fraction In Simplest Form
listenit
May 13, 2025 · 4 min read
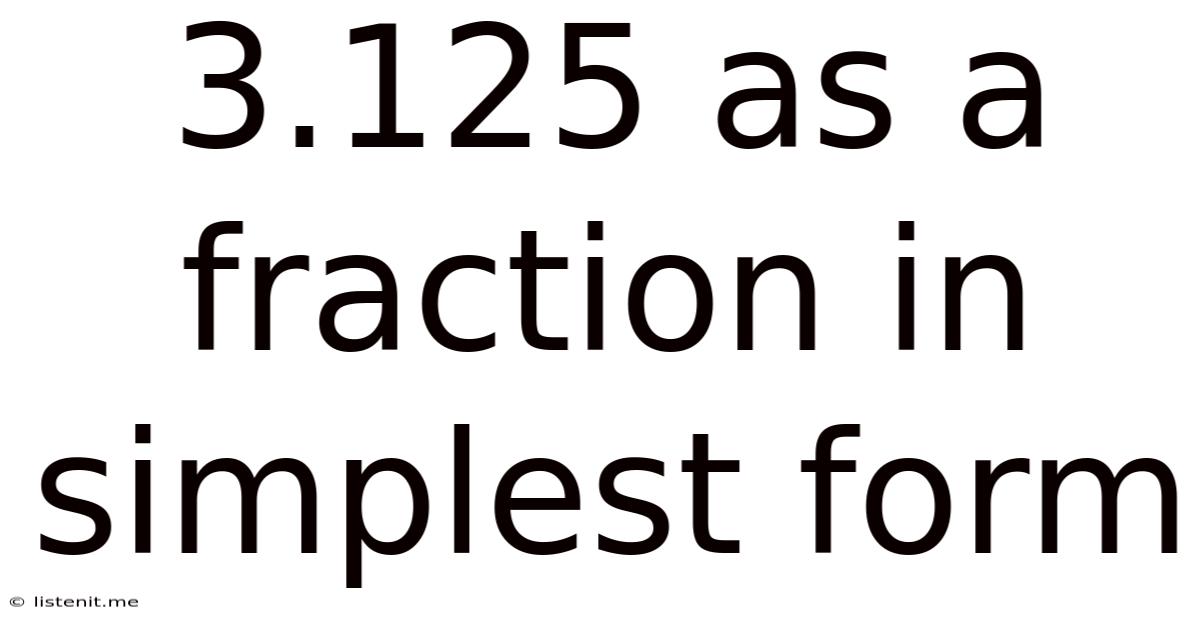
Table of Contents
3.125 as a Fraction in Simplest Form: A Comprehensive Guide
Converting decimals to fractions might seem daunting at first, but with a structured approach, it becomes a straightforward process. This comprehensive guide will walk you through the steps of converting 3.125 into its simplest fractional form, explaining the underlying principles and offering insights into handling similar decimal-to-fraction conversions. We'll delve into the methodology, explore practical applications, and address common misconceptions. By the end, you'll not only understand how to convert 3.125 but also possess the skills to tackle other decimal-to-fraction conversions with confidence.
Understanding Decimals and Fractions
Before we dive into the conversion, let's establish a strong foundation by reviewing the basics of decimals and fractions.
Decimals: Decimals represent numbers less than one using a base-ten system. The position of each digit after the decimal point represents a power of ten: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
Fractions: Fractions express a part of a whole, represented by a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts, while the denominator indicates the total number of equal parts the whole is divided into.
Converting 3.125 to a Fraction: Step-by-Step Guide
The conversion of 3.125 to a fraction involves several key steps:
Step 1: Identify the Place Value of the Last Digit
The last digit in 3.125 is 5, which occupies the thousandths place. This means our denominator will be 1000 (10 x 10 x 10).
Step 2: Write the Decimal as a Fraction
Represent the decimal portion (0.125) as a fraction using the denominator identified in Step 1:
0.125 = 125/1000
Step 3: Combine the Whole Number and Fractional Part
The number 3.125 has a whole number part (3) and a fractional part (125/1000). To combine them, we represent the whole number as an improper fraction with the same denominator:
3 = 3000/1000
Now, add the fractional parts:
3000/1000 + 125/1000 = 3125/1000
Step 4: Simplify the Fraction
The fraction 3125/1000 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of the numerator (3125) and the denominator (1000).
Finding the GCD can be done using various methods, such as prime factorization or the Euclidean algorithm. Let's use prime factorization:
- Prime factorization of 3125: 5 x 5 x 5 x 5 x 5 = 5<sup>5</sup>
- Prime factorization of 1000: 2 x 2 x 2 x 5 x 5 x 5 = 2<sup>3</sup> x 5<sup>3</sup>
The common factors are 5<sup>3</sup> (125). Dividing both the numerator and the denominator by 125:
3125 ÷ 125 = 25 1000 ÷ 125 = 8
Therefore, the simplified fraction is 25/8.
Verifying the Conversion
To ensure accuracy, we can convert the simplified fraction back into a decimal:
25 ÷ 8 = 3.125
This confirms that our conversion is correct.
Practical Applications of Decimal to Fraction Conversions
The ability to convert decimals to fractions is crucial in various fields:
- Engineering and Construction: Precise measurements and calculations often require fractional representations.
- Baking and Cooking: Recipes sometimes use fractional measurements, demanding accurate conversions.
- Finance: Calculating interest rates and portions of investments frequently involves fractions.
- Mathematics: Many mathematical operations are simplified when working with fractions instead of decimals.
Addressing Common Misconceptions
Here are a few common misconceptions surrounding decimal-to-fraction conversions:
- Incorrect simplification: Failing to find the greatest common divisor (GCD) results in an unsimplified fraction. Always ensure that you divide both the numerator and denominator by their GCD.
- Ignoring the whole number: Forcibly attempting to convert the entire decimal (including the whole number part) at once can lead to errors. Always handle the whole number and decimal parts separately before combining them.
- Confusion with recurring decimals: Recurring decimals (like 0.333...) require a slightly different approach than terminating decimals. They are converted using a specific algebraic technique.
Extending Your Skills: Handling More Complex Decimals
The techniques discussed above can be applied to more complex decimals. For instance, consider the decimal 12.375:
- Separate the whole number and the decimal: 12 and 0.375
- Convert the decimal to a fraction: 0.375 = 375/1000
- Simplify the fraction: 375/1000 simplified is 3/8
- Combine with the whole number: 12 + 3/8 = 96/8 + 3/8 = 99/8
The decimal 12.375, therefore, is represented as the fraction 99/8 in its simplest form.
Conclusion
Converting decimals to fractions is a fundamental skill with widespread applications. By following the systematic steps outlined above, you can confidently handle such conversions. Remember to always simplify your fraction to its lowest terms and verify your results. Mastering this skill not only enhances mathematical proficiency but also empowers you to tackle various real-world problems with precision and accuracy. Consistent practice will solidify your understanding and enable you to tackle even more complex decimal-to-fraction conversions with ease. Remember that understanding the underlying principles is key to mastering this skill, and with enough practice, you'll be a fraction conversion expert in no time.
Latest Posts
Latest Posts
-
Why Do Electric Field Lines Never Cross
May 13, 2025
-
1 10 As A Percent And Decimal
May 13, 2025
-
Can All Minerals Be A Gemstone
May 13, 2025
-
Multicellular Heterotrophs Without A Cell Wall
May 13, 2025
-
What Are The Gcf Of 48
May 13, 2025
Related Post
Thank you for visiting our website which covers about 3.125 As A Fraction In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.