2x Y 3 In Slope Intercept Form
listenit
May 10, 2025 · 4 min read
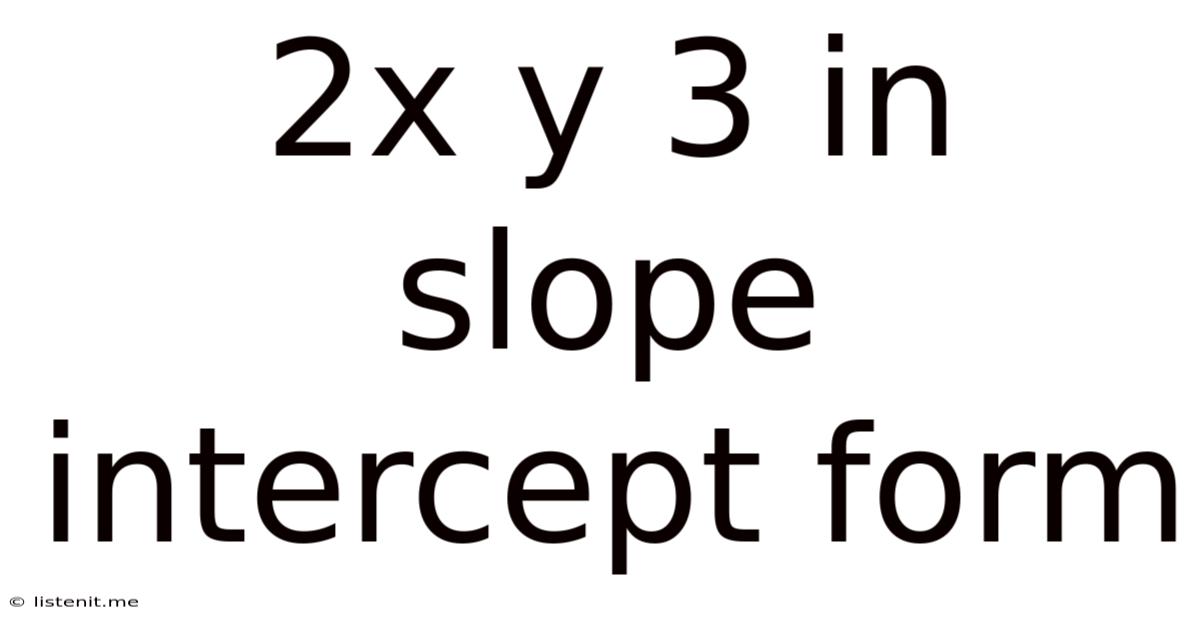
Table of Contents
Converting 2x + 3y = 6 to Slope-Intercept Form: A Comprehensive Guide
The equation 2x + 3y = 6 represents a straight line. However, it's not in the slope-intercept form, which is crucial for quickly understanding the line's characteristics – namely, its slope and y-intercept. This comprehensive guide will walk you through the process of converting this equation, explaining the underlying concepts and offering helpful tips for similar conversions. We'll also explore the significance of slope-intercept form and its applications in various mathematical contexts.
Understanding Slope-Intercept Form
The slope-intercept form of a linear equation is expressed as:
y = mx + b
Where:
- y represents the dependent variable (typically plotted on the vertical axis).
- x represents the independent variable (typically plotted on the horizontal axis).
- m represents the slope of the line, indicating its steepness and direction (positive slope indicates an upward trend, negative slope indicates a downward trend). The slope is calculated as the change in y divided by the change in x (rise over run).
- b represents the y-intercept, which is the point where the line intersects the y-axis (i.e., the value of y when x = 0).
Converting 2x + 3y = 6 to Slope-Intercept Form: A Step-by-Step Approach
To convert the equation 2x + 3y = 6 into slope-intercept form, we need to isolate 'y' on one side of the equation. Here's how:
-
Subtract 2x from both sides:
This step aims to move the 'x' term to the right side of the equation.
3y = -2x + 6
-
Divide both sides by 3:
This isolates 'y', giving us the equation in slope-intercept form.
y = (-2/3)x + 2
Now we have the equation in slope-intercept form: y = (-2/3)x + 2
Interpreting the Results: Slope and Y-Intercept
From the converted equation, we can easily identify the slope and y-intercept:
-
Slope (m) = -2/3: This indicates a negative slope. The line slopes downwards from left to right. For every 3 units increase in x, y decreases by 2 units.
-
Y-intercept (b) = 2: This means the line intersects the y-axis at the point (0, 2).
Graphical Representation
Plotting the line on a graph is a great way to visualize the equation. Start by plotting the y-intercept (0, 2). Then, use the slope (-2/3) to find another point. Since the slope is -2/3, you can move 3 units to the right and 2 units down from the y-intercept to find another point on the line (3, 0). Connect these two points to draw the line.
Applications of Slope-Intercept Form
The slope-intercept form is incredibly useful in various mathematical and real-world applications:
-
Predicting Values: Knowing the slope and y-intercept allows you to predict the value of y for any given value of x, and vice-versa.
-
Comparing Lines: It makes it easy to compare the steepness and direction of different lines. Lines with steeper slopes change more rapidly than lines with gentler slopes.
-
Modeling Real-World Phenomena: Linear equations in slope-intercept form are frequently used to model real-world relationships, such as the relationship between distance and time, cost and quantity, or temperature and altitude.
-
Solving Systems of Equations: The slope-intercept form can simplify the process of solving systems of linear equations graphically or algebraically. The point of intersection of two lines represents the solution to the system.
-
Linear Programming: In operations research, the slope-intercept form plays a critical role in linear programming problems, where the goal is to optimize a linear objective function subject to linear constraints.
Solving Related Problems: Practice Makes Perfect
Let's practice converting a few more equations into slope-intercept form:
Example 1: 4x - y = 8
- Add y to both sides: 4x = y + 8
- Subtract 8 from both sides: 4x - 8 = y
- Rewrite in slope-intercept form: y = 4x - 8
Example 2: x + 2y = 6
- Subtract x from both sides: 2y = -x + 6
- Divide both sides by 2: y = (-1/2)x + 3
Example 3: 3x + 6y = 12
- Subtract 3x from both sides: 6y = -3x + 12
- Divide both sides by 6: y = (-1/2)x + 2
Advanced Concepts and Extensions
While the slope-intercept form is extremely valuable, it's important to understand its limitations. Not all linear equations can be easily expressed in this form. For instance, a vertical line (x = a constant) has an undefined slope and cannot be written in slope-intercept form. Similarly, a horizontal line (y = a constant) has a slope of zero.
Conclusion: Mastering Slope-Intercept Form for Success
The conversion of 2x + 3y = 6 to slope-intercept form, y = (-2/3)x + 2, showcases the power and simplicity of this fundamental concept in algebra. Understanding slope-intercept form is essential for mastering linear equations and their applications in various fields. By practicing the steps outlined in this guide and tackling additional examples, you'll strengthen your understanding and confidently handle similar conversions in the future. Remember to always visualize the line graphically to reinforce your comprehension. This comprehensive approach will enable you to not only solve problems but also to deeply understand the underlying mathematical principles. The ability to manipulate and interpret linear equations is a cornerstone of further mathematical studies and real-world problem-solving.
Latest Posts
Latest Posts
-
In Which Medium Will Sound Waves Travel The Fastest
May 10, 2025
-
Atoms With The Same Atomic Number But Different Atomic Masses
May 10, 2025
-
Which Of The Following Atoms Is The Smallest
May 10, 2025
-
5 11x 2 3x 1 6x 189
May 10, 2025
-
Is Cos X Even Or Odd
May 10, 2025
Related Post
Thank you for visiting our website which covers about 2x Y 3 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.