2x X 3 What Is X
listenit
May 10, 2025 · 4 min read
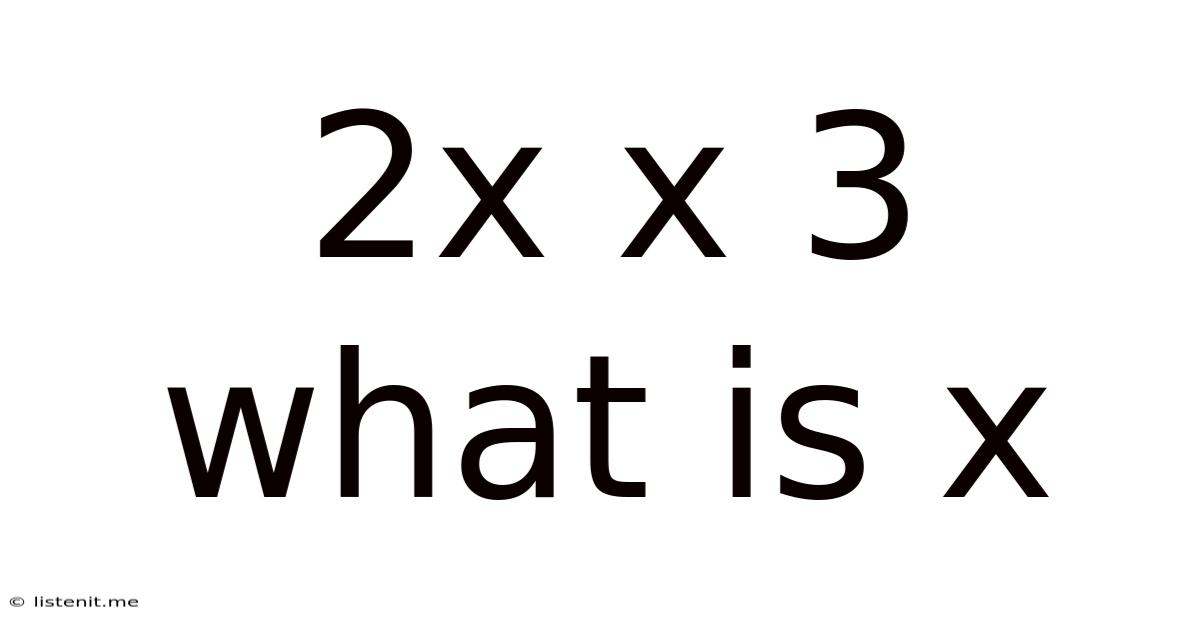
Table of Contents
2x * 3 = What is x? A Comprehensive Guide to Solving Algebraic Equations
This seemingly simple equation, 2x * 3 = ?, opens the door to a fundamental concept in algebra: solving for an unknown variable. Understanding how to solve for 'x' in this equation, and similar ones, is crucial for mastering algebra and numerous applications across various fields, from science and engineering to finance and economics. This guide will provide a detailed explanation of the solution, exploring various methods and extending the concept to more complex scenarios.
Understanding the Equation: 2x * 3
Before diving into the solution, let's break down the equation itself. We have:
2x * 3
This represents a mathematical expression where:
- x is an unknown variable, a value we need to determine.
- 2x means 2 multiplied by x.
- * 3 indicates that the result of 2x is further multiplied by 3.
The equation implies that the entire expression, 2x * 3, equals a certain value (which we'll explore in different scenarios below). Our goal is to isolate 'x' and find its value.
Solving for x: Method 1 - Step-by-Step Approach
The most straightforward approach involves performing inverse operations to isolate 'x'. Remember the order of operations (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). To solve for 'x', we'll work backward, using inverse operations:
-
Simplify the expression: First, we simplify the expression by multiplying 2x and 3:
2x * 3 = 6x
-
Introduce an equals sign: Now, let's assume the equation is 2x * 3 = 12. Our equation becomes:
6x = 12
-
Isolate x: To isolate 'x', we need to get rid of the 6 that's multiplying it. The inverse operation of multiplication is division. We divide both sides of the equation by 6:
6x / 6 = 12 / 6
-
Solve for x: This simplifies to:
x = 2
Therefore, if 2x * 3 = 12, then x = 2.
Solving for x: Method 2 - Distributive Property
Another approach involves using the distributive property, which states that a(b + c) = ab + ac. While this equation doesn't involve addition or subtraction within parentheses, we can still apply a variation of the distributive property. We can consider the equation as:
2 * (x * 3) = ?
Let's again assume the equation equals 12:
2 * (x * 3) = 12
We can then divide both sides by 2:
(x * 3) = 6
And finally divide both sides by 3:
x = 2
This method demonstrates the flexibility of algebraic manipulation.
Exploring Different Scenarios: Varying the Result
The beauty of algebraic equations lies in their ability to adapt to different scenarios. Let's explore what happens when the result of 2x * 3 changes:
Scenario 1: 2x * 3 = 18
- Simplify: 6x = 18
- Divide both sides by 6: x = 3
Scenario 2: 2x * 3 = 0
- Simplify: 6x = 0
- Divide both sides by 6: x = 0
Scenario 3: 2x * 3 = -6
- Simplify: 6x = -6
- Divide both sides by 6: x = -1
These examples showcase how the value of 'x' adapts to the given result, highlighting the dynamic nature of algebraic equations.
Extending the Concept: More Complex Equations
The fundamental principles we've explored can be extended to solve more complex equations. Let's consider an example:
3(2x + 5) = 27
To solve this:
- Distribute: Distribute the 3 to both terms inside the parentheses: 6x + 15 = 27
- Subtract 15: Subtract 15 from both sides: 6x = 12
- Divide by 6: Divide both sides by 6: x = 2
This example demonstrates how the same principles of inverse operations and simplification can be applied to more intricate algebraic expressions.
Real-World Applications
The ability to solve equations like 2x * 3 = ? is not confined to the classroom. It has numerous real-world applications:
- Engineering: Calculating dimensions, forces, and material properties.
- Finance: Determining interest rates, loan repayments, and investment returns.
- Physics: Solving problems related to motion, energy, and forces.
- Computer Science: Developing algorithms and solving computational problems.
- Economics: Modeling supply and demand, economic growth, and market equilibrium.
Conclusion: Mastering the Fundamentals
Solving for 'x' in the equation 2x * 3 = ? is a foundational step in mastering algebra. Through understanding the principles of inverse operations, the distributive property, and applying systematic methods, we can efficiently solve for the unknown variable in a range of scenarios. The ability to manipulate and solve algebraic equations is a critical skill with broad applications across numerous fields, making it an invaluable asset in academic and professional pursuits. By solidifying this fundamental understanding, you build a strong base for tackling more complex mathematical challenges and real-world problems. Remember to practice regularly, exploring different scenarios and equation types to enhance your proficiency. The more you practice, the more intuitive and efficient solving these types of equations will become.
Latest Posts
Latest Posts
-
2 3 To The Third Power
May 10, 2025
-
80 As A Fraction In Simplest Form
May 10, 2025
-
Find The Slope Of The Line Through P And Q
May 10, 2025
-
The Si Unit For Time Is
May 10, 2025
-
How Many Ways To Roll A 7 With 2 Dice
May 10, 2025
Related Post
Thank you for visiting our website which covers about 2x X 3 What Is X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.