2x 5y 10 Solve For Y
listenit
May 12, 2025 · 5 min read
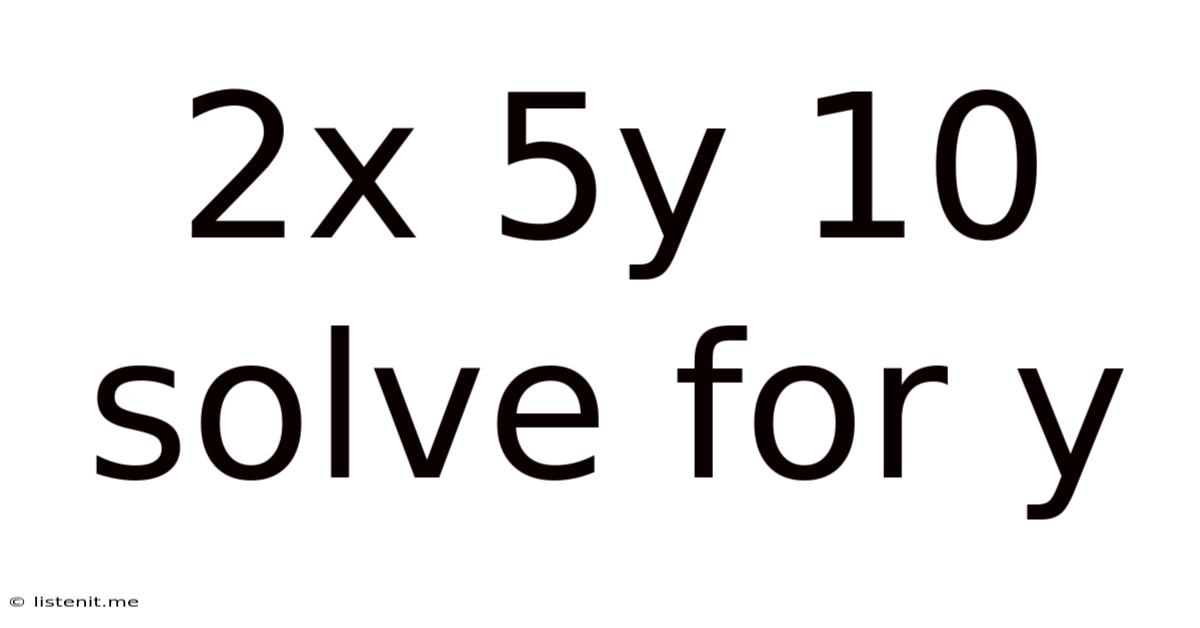
Table of Contents
Solving for 'y': A Comprehensive Guide to 2x + 5y = 10
This article provides a detailed explanation of how to solve the equation 2x + 5y = 10 for 'y', covering various approaches and highlighting crucial algebraic concepts. We'll explore the process step-by-step, emphasizing understanding over rote memorization. We'll also delve into the practical applications and implications of this seemingly simple equation, showcasing its relevance in diverse fields.
Understanding the Equation: 2x + 5y = 10
The equation 2x + 5y = 10 is a linear equation in two variables, 'x' and 'y'. This means that when graphed, it forms a straight line. Solving for 'y' means isolating 'y' on one side of the equation, expressing it in terms of 'x'. This gives us a function where the value of 'y' depends on the value of 'x'.
Key Concepts:
- Linear Equation: An equation where the highest power of the variables is 1.
- Variables: Symbols representing unknown quantities (in this case, 'x' and 'y').
- Constants: Fixed numerical values (in this case, 2, 5, and 10).
- Solving for a Variable: Manipulating the equation to isolate the desired variable on one side.
Method 1: Isolating 'y' through Algebraic Manipulation
This is the most common and straightforward method. The goal is to perform inverse operations to move all terms not involving 'y' to the right side of the equation.
Steps:
-
Subtract 2x from both sides: This eliminates '2x' from the left side. The equation becomes:
5y = 10 - 2x -
Divide both sides by 5: This isolates 'y'. The equation becomes:
y = (10 - 2x) / 5 -
Simplify (Optional): While this is already solved for 'y', you can simplify further by dividing each term in the numerator by 5:
y = 2 - (2/5)xory = 2 - 0.4x
This final equation, y = 2 - (2/5)x or y = 2 - 0.4x, explicitly shows 'y' as a function of 'x'. For any given value of 'x', you can calculate the corresponding value of 'y'.
Method 2: Using the Intercept Form
The intercept form of a linear equation is particularly useful for quickly identifying the x and y-intercepts of the line represented by the equation. The equation 2x + 5y = 10 can be rewritten in intercept form as follows:
- Divide the entire equation by 10: This normalizes the equation to the intercept form.
(2x/10) + (5y/10) = 10/10which simplifies to:(x/5) + (y/2) = 1
Now we can easily identify the x-intercept (where y = 0) and the y-intercept (where x = 0).
- x-intercept: When y = 0, x = 5. The x-intercept is (5, 0).
- y-intercept: When x = 0, y = 2. The y-intercept is (0, 2).
While this doesn't directly solve for 'y' in terms of 'x' in a single step as Method 1 does, it provides valuable insights into the line's characteristics and can be a helpful preliminary step. You can then rearrange the intercept form to solve for 'y' if needed:
(y/2) = 1 - (x/5)
y = 2 - (2/5)x or y = 2 - 0.4x (same result as Method 1)
Interpreting the Solution: y = 2 - (2/5)x
The solution, y = 2 - (2/5)x, represents a linear relationship between x and y. The equation describes a straight line with:
- y-intercept: 2 (when x = 0, y = 2)
- Slope: -2/5 (for every 5-unit increase in x, y decreases by 2 units). The negative slope indicates a downward trend.
This information is crucial for graphing the equation and understanding its implications.
Practical Applications
The equation 2x + 5y = 10, and the ability to solve it for 'y', has numerous practical applications across various fields:
-
Economics: This equation could represent a budget constraint, where 'x' and 'y' represent quantities of two goods, and 10 represents the total budget. Solving for 'y' allows one to determine how much of good 'y' can be purchased given a specific amount of good 'x'.
-
Physics: The equation might model a simple system involving two forces or variables related linearly. Solving for 'y' helps analyze the relationship between these variables.
-
Engineering: In various engineering applications, linear equations are used to model relationships between different variables. Solving for 'y' can aid in optimizing the system or understanding its behavior.
-
Computer Science: Linear equations are foundational in computer graphics, optimization algorithms, and machine learning. The ability to manipulate and solve these equations is essential.
Advanced Concepts and Extensions
While we've focused on the basic solution, several advanced concepts can build upon this understanding:
-
Systems of Equations: The equation 2x + 5y = 10 could be part of a system of equations with another equation involving 'x' and 'y'. Solving such a system involves finding values of 'x' and 'y' that satisfy both equations simultaneously. Techniques like substitution or elimination are employed for this purpose.
-
Linear Programming: In optimization problems, linear equations like 2x + 5y = 10 could represent constraints. Linear programming techniques are used to find the optimal values of 'x' and 'y' that maximize or minimize an objective function subject to these constraints.
-
Multivariate Equations: Extending the concept, one can encounter equations with more than two variables. Solving for one variable in terms of others requires similar algebraic manipulations.
-
Non-linear Equations: While this article focuses on linear equations, the principles of algebraic manipulation are applicable to solving for variables in non-linear equations as well, though the methods and techniques become more complex.
Conclusion: Mastering the Fundamentals
Solving the equation 2x + 5y = 10 for 'y' might seem like a simple task, but it represents a fundamental concept in algebra with far-reaching applications. Mastering this seemingly basic skill provides a solid foundation for tackling more complex mathematical problems across various disciplines. Understanding the underlying principles, rather than just memorizing steps, is key to effectively applying these concepts in real-world scenarios. By grasping the core ideas discussed here, you'll be well-equipped to tackle more challenging equations and problems in the future. The ability to manipulate equations and solve for variables is a critical skill for success in numerous academic and professional fields.
Latest Posts
Latest Posts
-
Why A Chemical Equation Must Be Balanced
May 13, 2025
-
A Parallelogram With A Right Angle
May 13, 2025
-
What Is The Ultimate Source Of Energy In Ecosystem
May 13, 2025
-
How To Know If A Molecule Is Soluble In Water
May 13, 2025
-
Are Diagonals Equal In A Rhombus
May 13, 2025
Related Post
Thank you for visiting our website which covers about 2x 5y 10 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.