27 Is 76 Of What Number
listenit
May 25, 2025 · 4 min read
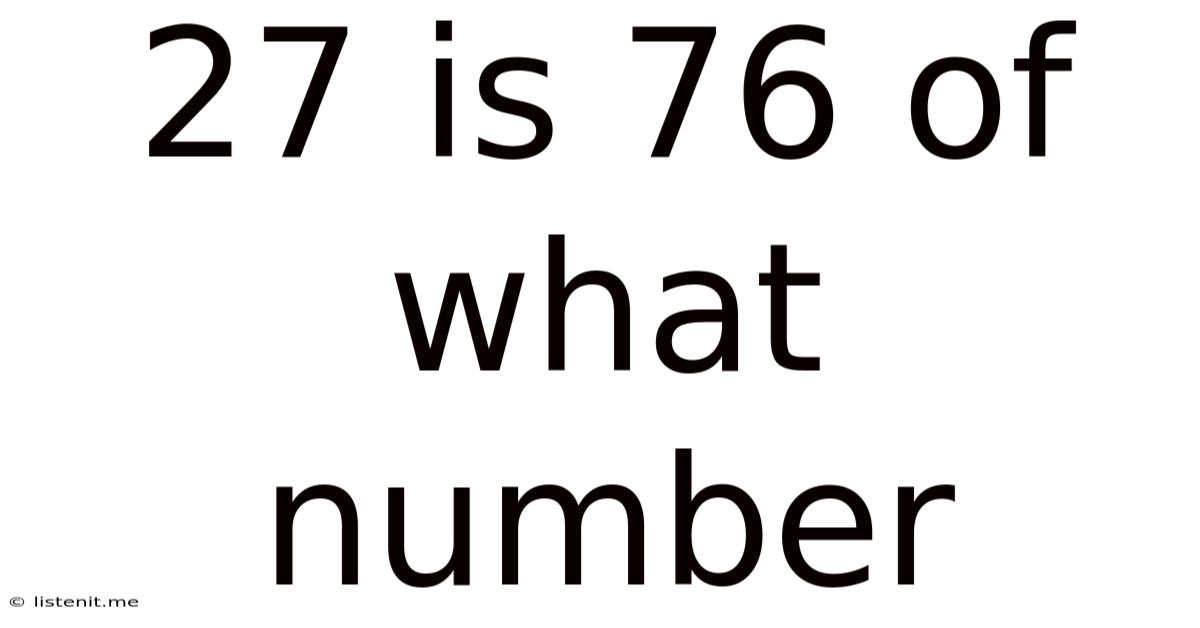
Table of Contents
27 is 76% of What Number? A Comprehensive Guide to Percentage Calculations
Finding an unknown number when you know a percentage and its corresponding value is a common mathematical problem. This article will comprehensively explore how to solve the problem "27 is 76% of what number?" We will not only provide the solution but also delve into the underlying principles, various methods for solving similar problems, and real-world applications of percentage calculations.
Understanding Percentages
Before diving into the solution, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a part of 100. The symbol "%" is used to denote percentages. For instance, 76% can be written as 76/100 or 0.76.
Percentages are used extensively in various fields, including:
- Finance: Calculating interest rates, discounts, profit margins, and taxes.
- Statistics: Representing data proportions and trends.
- Science: Expressing concentrations and experimental yields.
- Everyday life: Understanding sales, tips, and proportions in recipes.
Method 1: Using Proportions
The most straightforward approach to solving "27 is 76% of what number?" is by setting up a proportion. We can represent the problem as:
27 / x = 76 / 100
Where:
- 27 represents the given value.
- x represents the unknown number we're trying to find.
- 76/100 represents 76% as a fraction.
To solve for x, we cross-multiply:
27 * 100 = 76 * x
2700 = 76x
Now, divide both sides by 76:
x = 2700 / 76
x ≈ 35.53
Therefore, 27 is approximately 76% of 35.53.
Method 2: Using Decimal Equivalents
This method utilizes the decimal equivalent of the percentage. We know that 76% is equal to 0.76. We can rewrite the problem as:
27 = 0.76 * x
To solve for x, divide both sides by 0.76:
x = 27 / 0.76
x ≈ 35.53
This method yields the same result as the proportion method, confirming our answer.
Method 3: Algebraic Approach
We can also solve this using a straightforward algebraic equation. Let's represent the unknown number as 'x'. The problem can be translated into the following equation:
0.76x = 27
Dividing both sides by 0.76, we get:
x = 27 / 0.76
x ≈ 35.53
Again, we arrive at the same solution.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in various real-life scenarios. Here are some examples:
-
Sales and Discounts: If a store offers a 25% discount on an item originally priced at $80, you can use percentage calculations to determine the discounted price. ($80 * 0.25 = $20 discount; $80 - $20 = $60 final price).
-
Taxes: Calculating sales tax or income tax involves percentage calculations. If the sales tax rate is 6%, and you buy an item for $50, the tax amount is $50 * 0.06 = $3.
-
Investment Returns: If you invest $1000 and earn an 8% return, your profit would be $1000 * 0.08 = $80.
-
Grade Calculations: Many grading systems use percentages. If you scored 45 out of 60 on a test, your percentage score is (45/60) * 100 = 75%.
-
Surveys and Statistics: Percentages are frequently used to represent data in surveys and polls, helping to visualize and understand trends.
Expanding Your Knowledge: Solving for Different Variables
While this article focuses on finding the whole number when a percentage and its part are given, the principles can be applied to other percentage problems. For example:
-
Finding the Percentage: If you know the part and the whole, you can find the percentage. For example, if 15 is a part of 60, the percentage is (15/60) * 100 = 25%.
-
Finding the Part: If you know the whole and the percentage, you can find the part. For example, 20% of 150 is 150 * 0.20 = 30.
Advanced Percentage Calculations: Compound Interest and More
More complex scenarios involve compound interest, where interest is calculated not just on the principal amount but also on accumulated interest. This requires a more advanced formula, but the fundamental principles of percentage calculations remain the same.
Troubleshooting and Common Mistakes
-
Incorrect Decimal Conversion: Ensure you accurately convert percentages to decimals before performing calculations. 76% is 0.76, not 76.
-
Order of Operations: Follow the correct order of operations (PEMDAS/BODMAS) when solving equations to avoid errors.
-
Rounding Errors: Be mindful of rounding errors, especially when working with decimal numbers. In our example, 35.526 is approximately 35.53.
Conclusion
Solving "27 is 76% of what number?" is a simple yet fundamental percentage problem. Mastering this concept opens the door to understanding and solving a wide array of percentage-related problems in various fields. By understanding the different methods – proportions, decimal equivalents, and algebraic approaches – and practicing with diverse examples, you can build a solid foundation in percentage calculations and confidently tackle similar problems in the future. Remember to double-check your calculations and be aware of potential rounding errors to ensure accuracy.
Latest Posts
Latest Posts
-
6 Months From June 3 2024
May 25, 2025
-
100 100 100 100 100 100 100 100
May 25, 2025
-
How Tall Is 15 Feet Compared To A Human
May 25, 2025
-
What Is The Greatest Common Factor Of 45 And 30
May 25, 2025
-
What Is 5 2 Squared As A Fraction
May 25, 2025
Related Post
Thank you for visiting our website which covers about 27 Is 76 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.