250 Is What Percent Of 125
listenit
May 24, 2025 · 5 min read
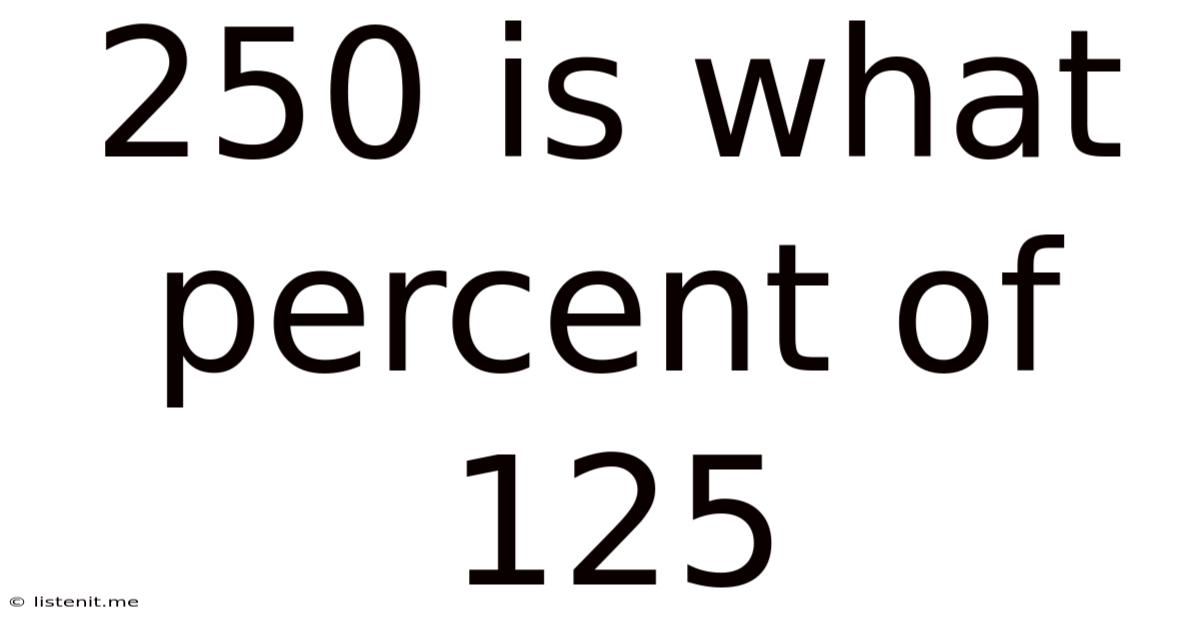
Table of Contents
250 is What Percent of 125? Understanding Percentage Calculations
This seemingly simple question, "250 is what percent of 125?", opens the door to a broader understanding of percentage calculations, a crucial skill in various aspects of life, from everyday budgeting to complex financial analysis. This article will not only answer the question directly but will also delve into the underlying mathematical principles, explore different methods for solving similar problems, and offer practical applications to solidify your understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ("per cent" in Latin). This means that 10% is equivalent to 10/100 or 1/10, 50% is 50/100 or 1/2, and 100% represents the whole. Understanding this fundamental concept is key to tackling percentage problems effectively.
Calculating "250 is What Percent of 125?"
To solve this problem, we need to find what percentage 250 represents when compared to 125. There are two primary methods to accomplish this:
Method 1: Using the Formula
The standard formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 250
- Whole: 125
Substituting these values into the formula:
(250 / 125) x 100% = 200%
Therefore, 250 is 200% of 125. This result might seem counterintuitive at first glance, as percentages are often thought of as being less than or equal to 100%. However, this result simply indicates that 250 is twice the size of 125.
Method 2: Using Proportions
Another approach involves setting up a proportion:
x/100 = 250/125
To solve for x (the percentage), cross-multiply:
125x = 25000
Then, divide both sides by 125:
x = 200
Therefore, again, 250 is 200% of 125.
Beyond the Basic Calculation: Practical Applications
Understanding percentage calculations extends far beyond solving simple mathematical problems. Here are some real-world scenarios where this skill is invaluable:
1. Financial Calculations
-
Interest Rates: Calculating simple and compound interest relies heavily on percentage calculations. Understanding how interest accrues is crucial for managing loans, investments, and savings accounts. For example, if you invest $1000 at a 5% annual interest rate, you'll earn $50 in interest after one year.
-
Discounts and Sales Tax: Retailers frequently advertise discounts as percentages. Being able to quickly calculate the final price after a discount (e.g., 20% off a $50 item) saves time and ensures you're getting the best deal. Similarly, understanding sales tax percentages allows you to accurately estimate the total cost of a purchase.
-
Profit Margins: Businesses use percentage calculations to determine their profit margins – the percentage of revenue remaining after deducting costs. This metric helps assess the profitability of products or services.
-
Investment Returns: Investors track their investment performance using percentages. A return of 10% means your investment grew by 10% of its initial value.
2. Everyday Life
-
Tip Calculations: Calculating a tip in a restaurant is a common application of percentages. A 15% tip on a $50 meal is easily calculated as 0.15 x $50 = $7.50.
-
Budgeting: Allocating a percentage of your income to different spending categories (rent, food, entertainment, etc.) helps create a balanced budget and track your expenses effectively.
-
Recipe Adjustments: Scaling recipes up or down involves percentage calculations. If a recipe calls for 1 cup of flour and you want to double it, you increase the flour by 100%.
-
Grade Calculations: In many educational systems, grades are expressed as percentages. Understanding your grade percentage provides insights into your academic performance.
3. Data Analysis
-
Data Interpretation: Percentage changes are frequently used to present and interpret data in various fields, including finance, science, and marketing. For example, analyzing the percentage increase in sales from one year to another reveals trends and growth patterns.
-
Statistical Analysis: Statistics relies heavily on percentages to represent probabilities, frequencies, and proportions in datasets.
Advanced Percentage Calculations
While the "250 is what percent of 125?" problem provides a foundational understanding, there are more complex percentage calculations you may encounter:
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. The formula is:
((New Value - Old Value) / Old Value) x 100%. For example, if sales increased from $1000 to $1200, the percentage increase is ((1200-1000)/1000) x 100% = 20%. -
Percentage Points: It's crucial to distinguish between percentage change and percentage points. A change from 10% to 20% is a 100% increase (as calculated above), but it's also a 10 percentage point increase.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The best way to master percentage calculations is to practice regularly with different types of problems. Start with basic examples and gradually move towards more complex ones.
-
Use Online Calculators and Resources: While understanding the underlying principles is crucial, online percentage calculators can be helpful for quick calculations and checking your work.
-
Break Down Complex Problems: If you're dealing with a complex percentage problem, break it down into smaller, more manageable steps.
-
Understand the Context: Always consider the context of the problem. Understanding what the numbers represent will help you interpret the results accurately.
-
Check Your Work: Always double-check your answers to ensure accuracy. A simple error in calculation can lead to incorrect conclusions.
Conclusion: The Power of Percentage Calculations
The seemingly simple question, "250 is what percent of 125?", serves as a gateway to a wide range of practical applications of percentage calculations. Mastering this skill is essential for success in various fields, from personal finance to data analysis. By understanding the underlying principles, practicing regularly, and utilizing available resources, you can confidently tackle percentage problems and leverage this fundamental skill in your daily life and professional endeavors. Remember that consistently practicing will build your confidence and proficiency in this essential mathematical area. The more you work with percentages, the more intuitive they will become.
Latest Posts
Latest Posts
-
How Many Months Until February 24 2025
May 24, 2025
-
What Is 1 9 As A Fraction
May 24, 2025
-
4 1 5 As An Improper Fraction
May 24, 2025
-
What Is 1 Divided By 9
May 24, 2025
-
What Time Will It Be In 20
May 24, 2025
Related Post
Thank you for visiting our website which covers about 250 Is What Percent Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.