25 Out Of 50 As A Percentage
listenit
May 26, 2025 · 5 min read
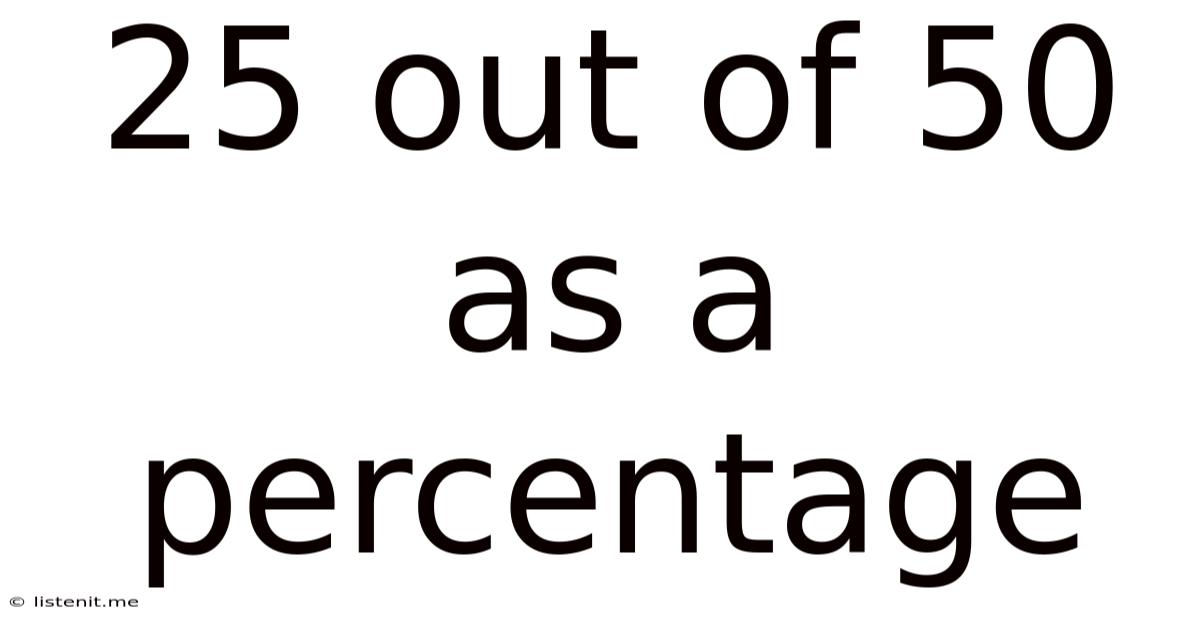
Table of Contents
25 out of 50 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from academic assessments to financial transactions and everyday decision-making. This comprehensive guide will delve into the specifics of calculating percentages, focusing particularly on determining what 25 out of 50 represents as a percentage. We'll explore multiple methods, address common misconceptions, and provide practical applications to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" – the symbol "%" representing this division. Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal.
Calculating 25 out of 50 as a Percentage: Three Methods
There are several ways to calculate the percentage represented by 25 out of 50. Let's explore three common approaches:
Method 1: The Fraction Method
This is arguably the most straightforward method. We can express "25 out of 50" as a fraction: 25/50. To convert this fraction to a percentage, we need to find an equivalent fraction with a denominator of 100.
- Simplify the fraction: 25/50 simplifies to 1/2 by dividing both the numerator and the denominator by 25.
- Convert to a percentage: To get a denominator of 100, we multiply both the numerator and denominator by 50 (1/2 * 50/50 = 50/100). This gives us 50/100, which is equivalent to 50%.
Method 2: The Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100.
- Convert the fraction to a decimal: 25/50 = 0.5 (divide 25 by 50).
- Convert the decimal to a percentage: Multiply the decimal by 100: 0.5 * 100 = 50%. Remember to add the "%" symbol to indicate a percentage.
Method 3: The Proportion Method
This method uses the concept of proportions to solve the problem. We can set up a proportion:
- Set up the proportion: 25/50 = x/100, where 'x' represents the percentage we're trying to find.
- Cross-multiply: 50x = 2500
- Solve for x: x = 2500/50 = 50%
All three methods yield the same result: 25 out of 50 is equivalent to 50%.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples demonstrating the application of this knowledge:
-
Academic Performance: If a student answers 25 out of 50 questions correctly on a test, their score is 50%. This allows for easy comparison with other students and assessment of their understanding.
-
Sales and Discounts: A store offering a 50% discount on an item means that the customer pays half the original price. Understanding percentages helps consumers quickly calculate the final price after a discount.
-
Financial Calculations: Interest rates, loan repayments, and investment returns are all expressed as percentages. Understanding percentages is essential for making informed financial decisions.
-
Statistical Analysis: Percentages are fundamental in presenting and interpreting statistical data. For instance, understanding the percentage of a population holding a particular view is crucial for market research and social analysis.
-
Recipe Scaling: If a recipe calls for 25g of an ingredient out of a total of 50g, you know you're using 50% of that ingredient. This is invaluable for adjusting recipe sizes.
Common Mistakes to Avoid When Calculating Percentages
While percentage calculations are relatively simple, several common mistakes can lead to inaccurate results. Here are some pitfalls to avoid:
-
Incorrect Fraction Setup: Ensure you accurately represent the given information as a fraction. The "out of" part represents the denominator, while the number before "out of" is the numerator.
-
Improper Simplification: Always simplify fractions before converting to percentages. This simplifies the calculation and minimizes errors.
-
Forgetting to Multiply by 100: When converting a decimal to a percentage, remember to multiply the decimal by 100. This is a crucial step often overlooked.
-
Misinterpreting Percentage Increases/Decreases: Understanding the difference between a percentage increase and a percentage decrease is crucial. A 50% increase from 50 is different from a 50% decrease from 100.
Beyond the Basics: More Complex Percentage Calculations
While 25 out of 50 is a straightforward calculation, the principles can be extended to more complex scenarios:
-
Calculating percentages of larger numbers: The same methods apply when calculating percentages of numbers greater than 100. For example, finding 25% of 200 involves multiplying 200 by 0.25.
-
Finding the original value: If you know the percentage and the resulting value, you can work backward to find the original value. For example, if 50% of a number is 25, then the original number is 50 (25 / 0.5 = 50).
-
Calculating percentage changes: This involves determining the percentage increase or decrease between two values. The formula typically involves subtracting the initial value from the final value, dividing the result by the initial value, and multiplying by 100.
-
Compound percentages: This deals with situations where a percentage change is applied multiple times. For instance, calculating the final value after applying a 10% increase followed by a 5% decrease requires understanding how these percentages compound.
Conclusion: Mastering Percentages for Everyday Success
The ability to calculate percentages accurately is a valuable skill applicable across numerous fields. While calculating 25 out of 50 as a percentage (50%) is a simple exercise, mastering the underlying principles allows you to confidently tackle more complex percentage problems in various contexts, from managing your finances to analyzing data or even understanding complex statistics in the news. Remember to avoid common pitfalls, practice regularly, and apply your knowledge in real-world scenarios to solidify your understanding. By understanding percentages thoroughly, you'll enhance your analytical capabilities and make informed decisions in many areas of your life.
Latest Posts
Latest Posts
-
People With Muscle Dysmorphia Tend To
May 27, 2025
-
Is Sorbitol The Same As Xylitol
May 27, 2025
-
What Is The Half Life Of Aspirin
May 27, 2025
-
The Contractile Unit Of A Myofibril Is Called The
May 27, 2025
-
Do You Still Have Graves Disease After Radioactive Iodine Treatment
May 27, 2025
Related Post
Thank you for visiting our website which covers about 25 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.