25 3 As A Mixed Number
listenit
May 12, 2025 · 4 min read
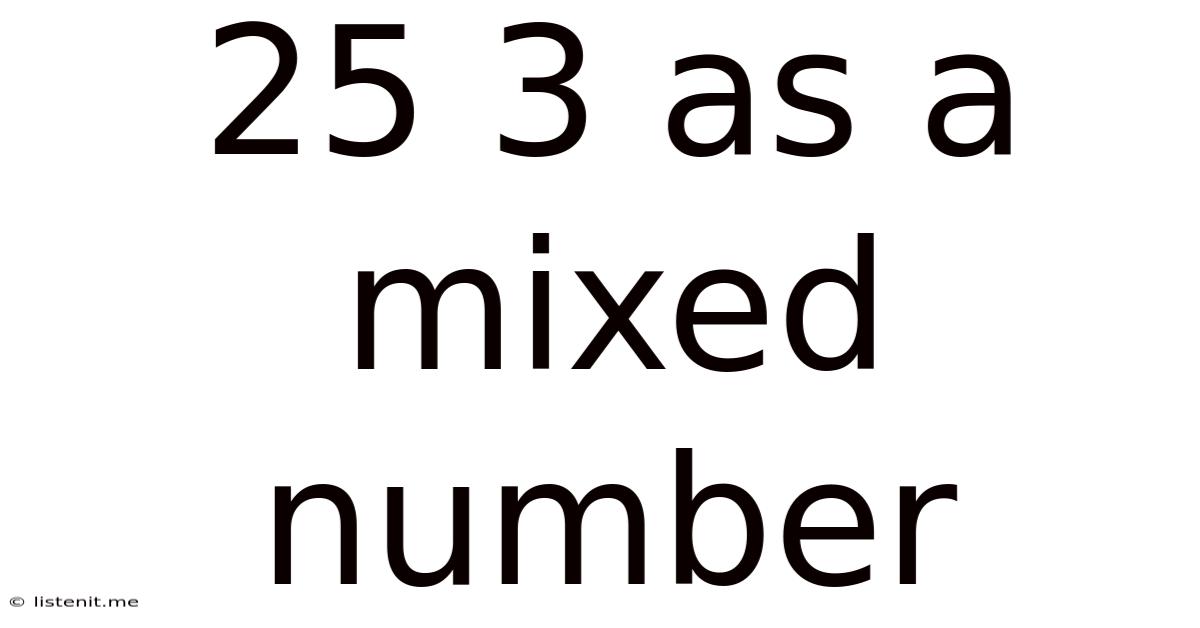
Table of Contents
25/3 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the conversion of the improper fraction 25/3 into a mixed number, explaining the process step-by-step and providing additional examples and practice problems to solidify your understanding. We'll also explore the broader context of improper fractions and mixed numbers, highlighting their applications in various mathematical contexts.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ½, 2 ¾, and 5 ⅛ are all mixed numbers. They represent a quantity greater than one.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Examples include 7/4, 11/5, and 25/3. These fractions represent a quantity greater than or equal to one.
Converting an Improper Fraction to a Mixed Number: The Process
The core of this article revolves around converting the improper fraction 25/3 into a mixed number. The process involves division:
- Divide the numerator by the denominator: Divide 25 by 3.
- Determine the whole number: The quotient (result of the division) becomes the whole number part of the mixed number. 25 divided by 3 is 8 with a remainder of 1. Therefore, the whole number is 8.
- Determine the fractional part: The remainder becomes the numerator of the fractional part, and the original denominator remains the same. The remainder is 1, and the denominator is 3. This gives us the fraction 1/3.
- Combine the whole number and the fraction: Combine the whole number (8) and the fraction (1/3) to create the mixed number. Therefore, 25/3 as a mixed number is 8 ⅓.
Visualizing the Conversion
Imagine you have 25 identical objects. If you want to group them into sets of 3, you can create 8 complete sets (8 x 3 = 24 objects) with 1 object remaining. This visually represents the 8 whole numbers and the remaining 1/3.
Why is this Conversion Important?
Converting improper fractions to mixed numbers is crucial for several reasons:
- Improved Understanding: Mixed numbers often provide a more intuitive understanding of quantities than improper fractions. It's easier to grasp the concept of "8 and one-third" than "twenty-five thirds."
- Easier Calculations: In many mathematical operations, especially addition and subtraction, working with mixed numbers can simplify the process.
- Real-World Applications: Mixed numbers frequently appear in everyday life, from measuring ingredients in recipes to calculating distances and quantities.
Practice Problems: Converting Improper Fractions to Mixed Numbers
Let's solidify your understanding with some practice problems:
- Convert 17/5 to a mixed number. (Solution: 3 ⅖)
- Convert 22/7 to a mixed number. (Solution: 3 ⅛)
- Convert 31/4 to a mixed number. (Solution: 7 ¾)
- Convert 47/6 to a mixed number. (Solution: 7 ⁵⁄₆)
- Convert 59/8 to a mixed number. (Solution: 7 ⅜)
Converting Mixed Numbers to Improper Fractions
The reverse process, converting a mixed number back to an improper fraction, is equally important. To convert a mixed number (like 8 ⅓) to an improper fraction:
- Multiply the whole number by the denominator: 8 x 3 = 24
- Add the numerator: 24 + 1 = 25
- Keep the denominator the same: The denominator remains 3.
- Combine to form the improper fraction: The resulting improper fraction is 25/3.
Advanced Applications and Further Exploration
The conversion between improper fractions and mixed numbers extends beyond basic arithmetic. They are essential in:
- Algebra: Solving equations and inequalities often involves working with fractions, requiring the ability to convert between improper fractions and mixed numbers.
- Geometry: Calculating areas, volumes, and other geometric properties often necessitates the use of fractions.
- Calculus: Derivatives and integrals frequently involve fractional expressions.
- Data Analysis: Representing and interpreting data, especially proportions and ratios, often requires understanding and manipulating fractions.
Common Mistakes to Avoid
- Incorrect Division: Ensure you accurately divide the numerator by the denominator. A small error in division will lead to an incorrect mixed number.
- Forgetting the Remainder: Don't forget to include the remainder as the numerator of the fractional part of the mixed number.
- Incorrectly Combining Whole Number and Fraction: Make sure you correctly combine the whole number obtained from the division with the fraction formed from the remainder and the original denominator.
Conclusion
Converting the improper fraction 25/3 to the mixed number 8 ⅓ is a fundamental skill in mathematics with widespread applications. Understanding this process, along with the broader concepts of improper fractions and mixed numbers, is vital for success in various mathematical contexts and real-world situations. By mastering this skill, you'll enhance your mathematical proficiency and problem-solving abilities. Remember to practice regularly to build confidence and accuracy. The provided practice problems should help you to hone your skills and ensure a firm grasp of this important mathematical concept. Remember, consistent practice is key to mastering any mathematical skill. Keep practicing and you'll soon find these conversions second nature.
Latest Posts
Latest Posts
-
The Solubilities Of Three Salts In Water
May 12, 2025
-
How To Find Volume Of Rock
May 12, 2025
-
A Tennis Court Is 78 Feet Long And
May 12, 2025
-
How To Find A Vector Parallel To Another Vector
May 12, 2025
-
What Is The Reciprocal Of 4 3
May 12, 2025
Related Post
Thank you for visiting our website which covers about 25 3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.