24 Is What Percent Of 200
listenit
May 25, 2025 · 4 min read
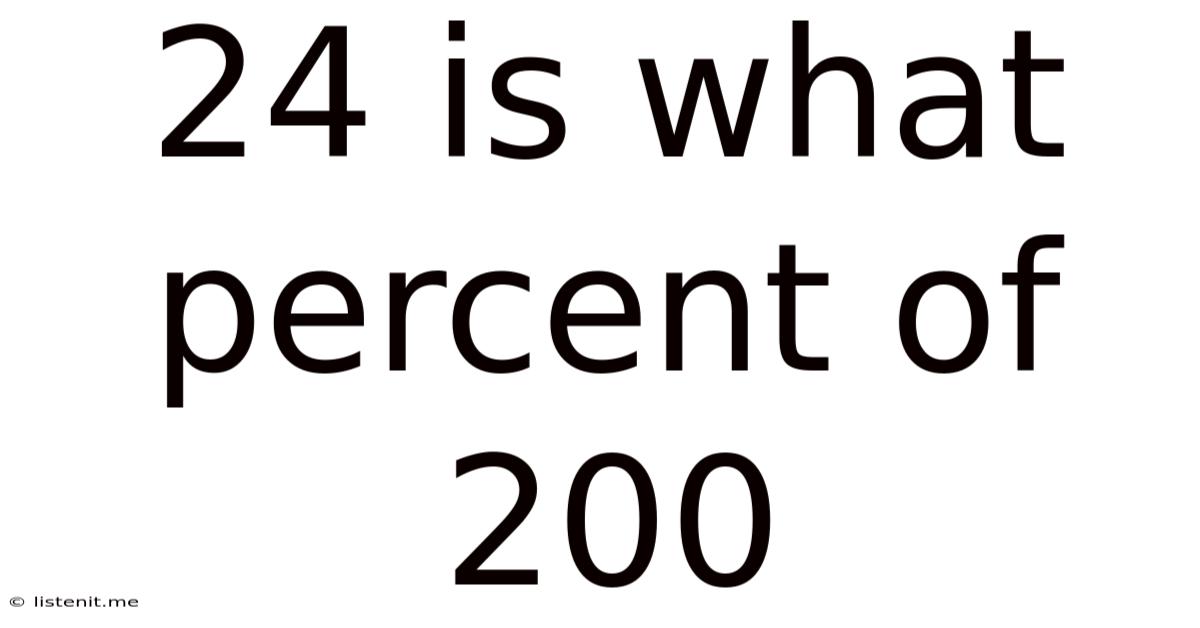
Table of Contents
24 is What Percent of 200? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article delves into the question, "24 is what percent of 200?", providing a step-by-step solution, exploring different calculation methods, and demonstrating the practical applications of percentage calculations. We'll also explore related concepts and offer tips for mastering percentage problems.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used extensively to represent proportions, ratios, and changes in values.
Calculating "24 is What Percent of 200?"
There are several ways to solve this problem. Let's explore two common methods:
Method 1: Using the Formula
The basic formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 24
- Whole: 200
Substituting these values into the formula:
(24 / 200) * 100% = 12%
Therefore, 24 is 12% of 200.
Method 2: Proportion Method
This method involves setting up a proportion:
x/100 = 24/200
where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
200x = 2400
Then, divide both sides by 200:
x = 2400 / 200 = 12
Therefore, x = 12%, confirming our previous result.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios:
1. Financial Calculations:
- Discounts: Determining the final price of an item after a percentage discount. For example, a 20% discount on a $100 item means a $20 reduction, resulting in a final price of $80.
- Interest Rates: Calculating simple and compound interest on loans, savings accounts, and investments.
- Taxes: Determining the amount of tax payable on income, sales, or property.
- Profit Margins: Calculating the percentage of profit earned on sales.
- Investment Returns: Tracking the percentage growth or decline in investment portfolios.
2. Statistical Analysis:
- Data Representation: Percentages are used to represent proportions within datasets, making it easier to compare and interpret data.
- Probability: Expressing the likelihood of events occurring as percentages.
- Surveys and Polls: Presenting survey results and poll data using percentages to show the distribution of responses.
3. Everyday Life:
- Tip Calculations: Determining the appropriate tip amount in restaurants based on a percentage of the bill.
- Sales Tax: Calculating the total cost of an item including sales tax.
- Grading Systems: Converting numerical scores into percentage grades.
- Recipe Scaling: Adjusting ingredient quantities in recipes based on percentages.
Advanced Percentage Problems & Concepts
While the "24 is what percent of 200?" problem is relatively straightforward, percentage calculations can become more complex. Here are some advanced concepts:
1. Percentage Increase and Decrease:
Calculating the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100%
A positive result indicates an increase, while a negative result indicates a decrease.
2. Percentage Points:
This is often confused with percentages. Percentage points refer to the arithmetic difference between two percentages, not the percentage change. For example, an increase from 10% to 15% is a 5-percentage point increase, but a 50% percentage increase.
3. Compounding Percentages:
This involves calculating the effect of successive percentage changes. For example, calculating the final value after applying multiple discounts or interest rates consecutively.
4. Solving for the Whole or Part:
The basic percentage formula can be rearranged to solve for the whole or the part if the percentage and one of the other values are known.
Tips for Mastering Percentage Calculations
- Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations.
- Understand the Formula: Make sure you thoroughly understand the basic percentage formula and its variations.
- Use a Calculator: A calculator can save you time and improve accuracy, especially with more complex problems.
- Check Your Work: Always double-check your answers to avoid errors.
- Break Down Complex Problems: Divide complex percentage problems into smaller, manageable steps.
Conclusion
Understanding percentages is a vital skill applicable in various aspects of life. The simple problem of "24 is what percent of 200?" serves as a foundation for understanding more complex percentage calculations. By mastering these concepts and utilizing the methods outlined above, you can confidently tackle percentage problems and apply them effectively in diverse situations. Remember to practice regularly and utilize the tips provided to enhance your proficiency and accuracy in solving percentage-related challenges. This improved understanding will benefit your academic pursuits, professional endeavors, and everyday life.
Latest Posts
Latest Posts
-
Round 769 68055077 To The Nearest Hundred
May 25, 2025
-
How Many Days Has It Been Since May 31
May 25, 2025
-
6409 Divided By 61 As A Fraction
May 25, 2025
-
How Long Ago Was 18 Years Ago
May 25, 2025
-
What Is The Percentage Of 3 Out Of 4
May 25, 2025
Related Post
Thank you for visiting our website which covers about 24 Is What Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.