23 Out Of 50 As A Percentage
listenit
May 24, 2025 · 4 min read
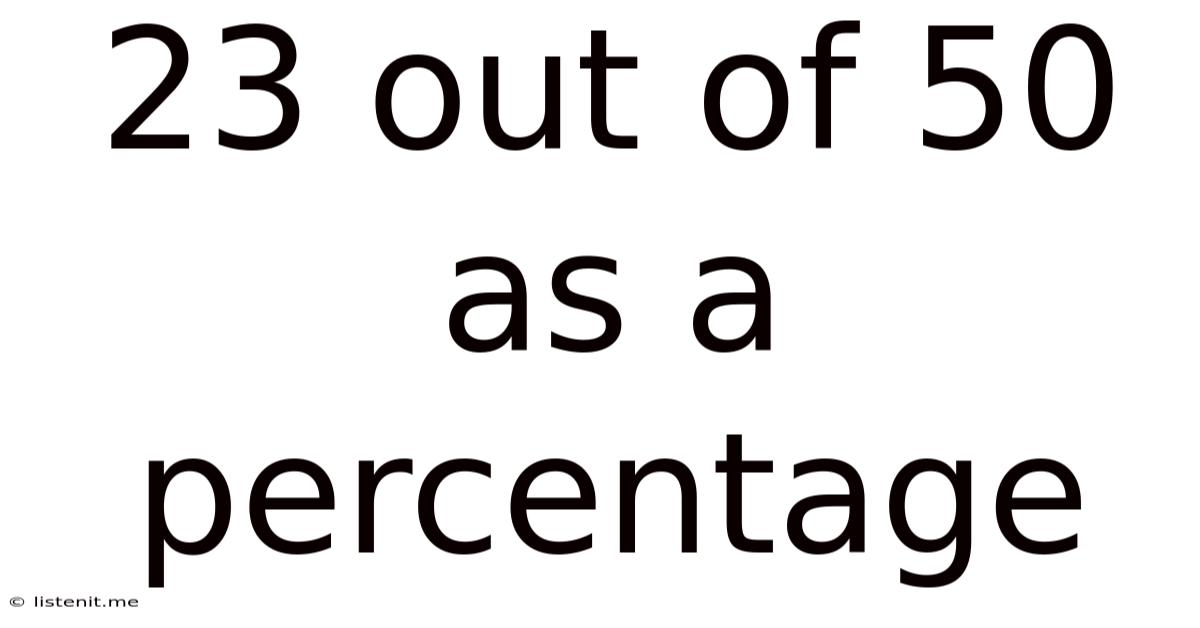
Table of Contents
23 out of 50 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assignments and financial planning to everyday decision-making. Understanding how to convert fractions to percentages is crucial for interpreting data, making comparisons, and solving problems efficiently. This in-depth guide will not only show you how to calculate 23 out of 50 as a percentage but also provide you with the broader context and various methods for tackling similar percentage problems.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The word "percent" itself originates from the Latin "per centum," meaning "out of a hundred." Therefore, expressing a value as a percentage signifies its proportion relative to a whole that's considered 100 units.
Method 1: Using the Basic Percentage Formula
The most straightforward method to determine 23 out of 50 as a percentage involves applying the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 23 (the number we're considering as a fraction of the whole)
- Whole: 50 (the total number representing the whole)
Let's plug the values into the formula:
(23 / 50) x 100% = 46%
Therefore, 23 out of 50 is 46%.
Method 2: Converting the Fraction to a Decimal
Another effective method involves converting the fraction 23/50 into a decimal and then multiplying by 100%.
-
Divide the numerator by the denominator: 23 ÷ 50 = 0.46
-
Multiply the decimal by 100%: 0.46 x 100% = 46%
This method confirms that 23 out of 50 is indeed 46%.
Method 3: Using Proportions
The concept of proportions offers a slightly different approach to solving this type of problem. A proportion is an equation stating that two ratios are equal. We can set up a proportion to find the percentage:
23/50 = x/100
Here, 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
23 x 100 = 50 x x
2300 = 50x
x = 2300 / 50
x = 46
Therefore, x = 46%, confirming our previous results.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a variety of real-world scenarios. Here are just a few examples:
1. Academic Performance:
Imagine a student scored 23 out of 50 on a test. Knowing that this equates to 46% allows the student to understand their performance relative to the total possible marks. This understanding helps them gauge their progress and identify areas for improvement.
2. Financial Calculations:
Percentages are essential for calculating discounts, interest rates, taxes, and profit margins. For example, a 46% discount on a product can be quickly calculated using the percentage.
3. Data Analysis and Interpretation:
In various fields like business, marketing, and research, analyzing data often involves working with percentages. Understanding percentages allows for easier interpretation of trends, comparisons between groups, and identification of significant patterns.
4. Everyday Life:
From calculating tips in restaurants to understanding sales tax, percentages are frequently encountered in daily life. The ability to quickly calculate percentages makes these everyday tasks much more efficient.
Beyond 23 out of 50: Mastering Percentage Calculations
The methods outlined above are adaptable to various percentage problems. To further enhance your skills, consider the following:
Handling Larger Numbers:
The same principles apply to more extensive numbers. For instance, to calculate 230 out of 500, you’d still use the formula (Part / Whole) x 100%. The result would remain 46%.
Calculating Percentages Greater Than 100%:
Situations may arise where the "part" is greater than the "whole." This results in a percentage exceeding 100%, indicating that the "part" surpasses the original "whole." The calculation method remains the same, but the interpretation differs.
Calculating the "Part" or "Whole" when the Percentage is Known:
The percentage formula can be rearranged to solve for the "part" or "whole" if the percentage and either the "part" or "whole" are known.
Tips and Tricks for Efficient Percentage Calculations
-
Memorizing Common Fractions and Their Percentage Equivalents: Knowing that 1/2 = 50%, 1/4 = 25%, 1/5 = 20%, etc., speeds up calculations.
-
Using a Calculator: For complex calculations, a calculator simplifies the process and minimizes errors.
-
Estimating Percentages: For quick estimations, round numbers to make mental calculations easier.
-
Practice Regularly: The more you practice solving percentage problems, the faster and more confident you'll become.
Conclusion
Calculating 23 out of 50 as a percentage is a fundamental skill with wide-ranging applications. Understanding the basic formula, alternative methods like using decimals and proportions, and mastering the application of percentages in various contexts enhances problem-solving abilities and facilitates a deeper understanding of numerical data. By practicing these techniques and exploring further applications, you’ll build confidence and proficiency in dealing with percentages across various aspects of life. Remember that consistent practice is key to mastering percentage calculations and applying them effectively in diverse situations.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 90 And 135
May 25, 2025
-
17 Out Of 22 Is What Percent
May 25, 2025
-
One Percent Of A Million Dollars
May 25, 2025
-
Whats The Prime Factorization Of 27
May 25, 2025
-
Usable Ip Addresses In A 30
May 25, 2025
Related Post
Thank you for visiting our website which covers about 23 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.