22 Is 25 Of What Number
listenit
May 09, 2025 · 5 min read
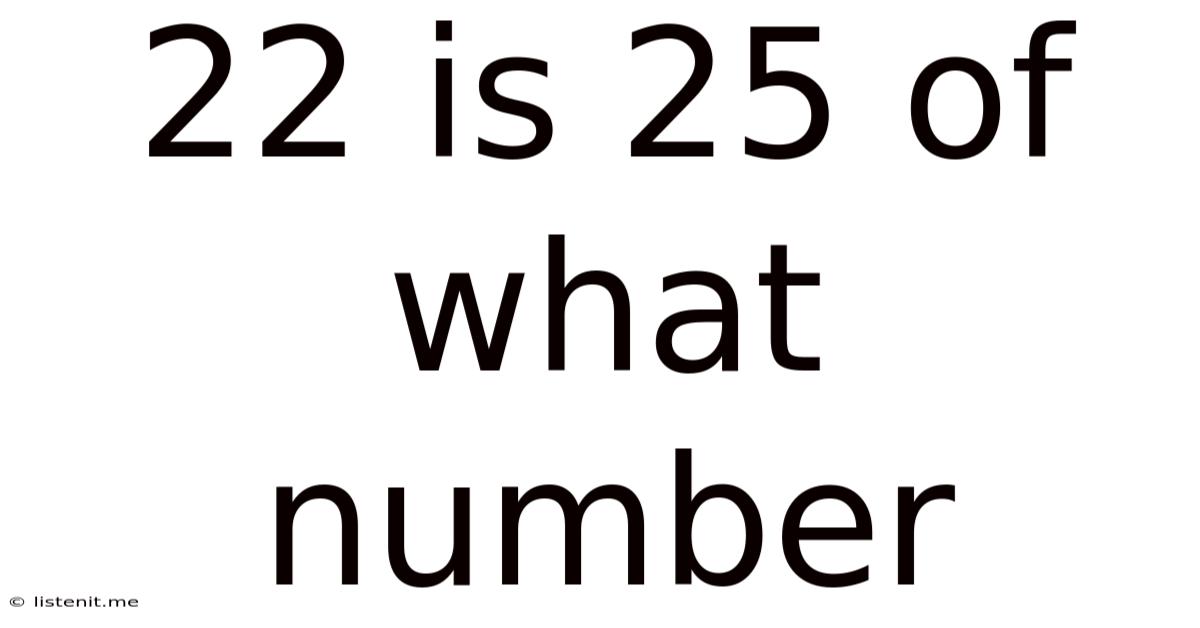
Table of Contents
22 is 25% of What Number? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "22 is 25% of what number?", opens the door to a deeper understanding of percentages, their applications, and how to solve various percentage-related problems. While the answer might seem straightforward at first glance, exploring the different methods for solving this problem reveals a wealth of mathematical concepts and practical applications. This article will guide you through multiple approaches, highlighting the underlying principles and showcasing the versatility of percentage calculations.
Understanding Percentages
Before delving into the solution, let's establish a firm grasp of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" denotes "per cent," meaning "out of one hundred." So, 25% literally means 25 out of 100, or 25/100, which simplifies to 1/4. This understanding forms the foundation for solving percentage problems.
Method 1: Using the Percentage Formula
The most common and straightforward method involves using the basic percentage formula:
Part = Percentage × Whole
In our problem, we know the "Part" (22) and the "Percentage" (25%). We need to find the "Whole." Let's represent the "Whole" with the variable 'x'. Substituting the known values into the formula, we get:
22 = 0.25 × x
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 0.25:
x = 22 / 0.25
x = 88
Therefore, 22 is 25% of 88.
Method 2: Using Proportions
Another effective method is to set up a proportion. A proportion expresses the equality of two ratios. We can represent the problem as:
22/x = 25/100
This proportion states that the ratio of 22 to the unknown number (x) is equal to the ratio of 25 to 100 (which is the definition of 25%). To solve for 'x', we can cross-multiply:
22 × 100 = 25 × x
2200 = 25x
Now, divide both sides by 25:
x = 2200 / 25
x = 88
Again, we find that 22 is 25% of 88.
Method 3: Working with Fractions
As mentioned earlier, 25% is equivalent to the fraction 1/4. We can rewrite the problem as:
22 = (1/4) × x
To solve for 'x', multiply both sides by 4:
x = 22 × 4
x = 88
This method demonstrates the direct relationship between percentages, decimals, and fractions.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios:
1. Financial Calculations:
- Interest Rates: Calculating interest earned on savings accounts or interest payable on loans heavily relies on percentage calculations.
- Discounts: Determining the final price of an item after a discount involves calculating a percentage reduction.
- Taxes: Calculating sales tax or income tax requires understanding percentages.
- Profit Margins: Businesses use percentages to calculate profit margins and track their financial performance.
- Investment Returns: Assessing the return on investment (ROI) involves percentage calculations.
2. Scientific and Statistical Applications:
- Data Analysis: Percentages are frequently used to represent proportions and trends within data sets.
- Probability and Statistics: Percentages are fundamental in expressing probabilities and statistical results.
- Scientific Measurements: Many scientific measurements involve percentages, such as percentage error or concentration levels.
3. Everyday Life Applications:
- Tip Calculations: Determining the appropriate tip amount in a restaurant involves calculating a percentage of the bill.
- Sales and Discounts: Evaluating deals and discounts requires understanding percentages.
- Recipe Adjustments: Scaling up or down recipes involves calculating percentage increases or decreases in ingredient quantities.
- Grading Systems: Many academic grading systems are based on percentages.
Expanding the Concept: Solving for Different Variables
The problem "22 is 25% of what number?" is a specific case. Let's explore how to solve for different variables in the percentage formula:
1. Finding the Percentage:
If we know the "Part" and the "Whole," we can find the "Percentage." For example, if 22 is a part of 88, what percentage is it?
Percentage = (Part / Whole) × 100
Percentage = (22 / 88) × 100
Percentage = 25%
2. Finding the Part:
If we know the "Percentage" and the "Whole," we can find the "Part." For example, what is 25% of 88?
Part = Percentage × Whole
Part = 0.25 × 88
Part = 22
Advanced Percentage Problems and Techniques
While the problem presented is relatively straightforward, more complex percentage problems exist, requiring a deeper understanding of mathematical operations and problem-solving strategies. These may include:
- Compound Interest: Calculating interest that accumulates on both the principal and accumulated interest.
- Percentage Change: Determining the percentage increase or decrease between two values.
- Percentage Point Difference: Distinguishing between percentage change and percentage point difference.
- Successive Percentage Changes: Calculating the overall percentage change after multiple consecutive percentage changes.
Mastering these advanced techniques requires practice and a solid foundation in basic percentage calculations.
Conclusion: The Power of Percentage Understanding
The seemingly simple question, "22 is 25% of what number?" serves as a gateway to a broad range of mathematical concepts and real-world applications. By understanding the different methods for solving this problem—using the percentage formula, proportions, or fractions—and recognizing the various practical applications of percentages, we can unlock a powerful tool for navigating numerous aspects of our daily lives, from personal finance to scientific research. The more comfortable you become with percentage calculations, the more confident and effective you will be in solving a wide array of quantitative problems. Remember that practice is key to mastering this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Drawing Bond Line Structures From Newman Projections
May 09, 2025
-
What Is 10 6 In Simplest Form
May 09, 2025
-
Is Pure Water A Mixture Or Pure Substance
May 09, 2025
-
Is S Or N More Electronegative
May 09, 2025
-
How To Write 3 8 As A Decimal
May 09, 2025
Related Post
Thank you for visiting our website which covers about 22 Is 25 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.