21 Out Of 27 As A Percentage
listenit
May 24, 2025 · 4 min read
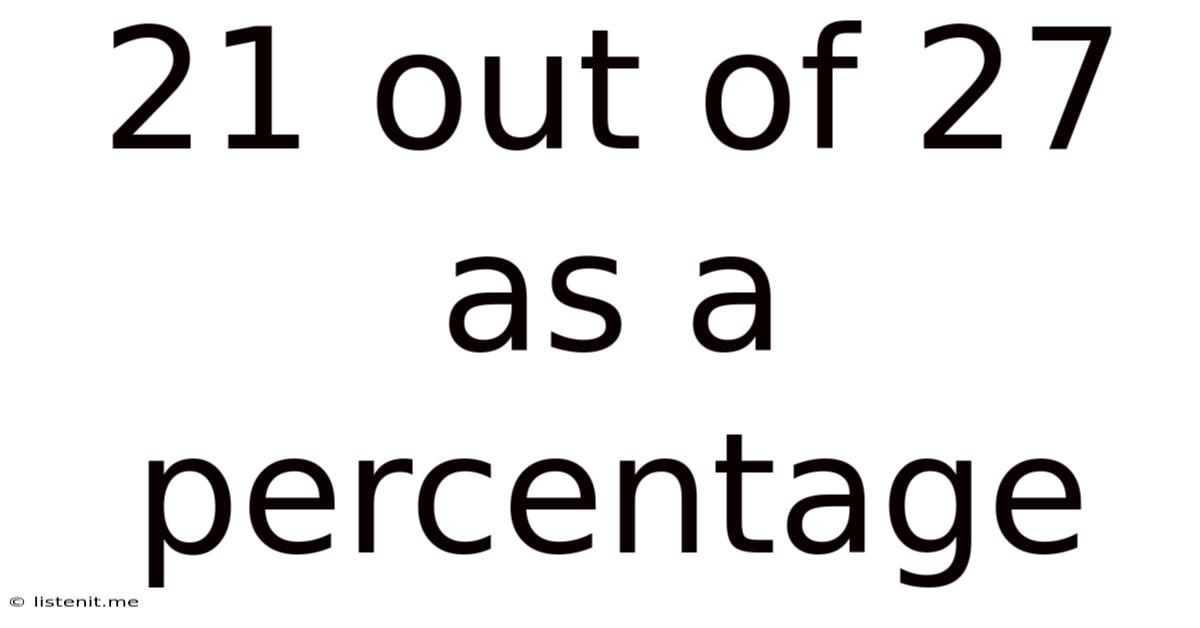
Table of Contents
21 out of 27 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic assessments to financial transactions and everyday decision-making. Understanding how to convert fractions into percentages allows for easier comparison and interpretation of data. This comprehensive guide will delve into the process of calculating "21 out of 27 as a percentage," exploring different methods and demonstrating their applications. We'll also discuss the importance of percentage calculations in various contexts and provide practical examples to solidify your understanding.
Understanding Percentages
Before we dive into the calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." Therefore, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
Percentages are used extensively because they provide a standardized way to compare different quantities. Whether it's comparing test scores, analyzing market shares, or calculating discounts, percentages offer a clear and easily understood representation of proportions.
Method 1: Using the Formula
The most straightforward method to calculate "21 out of 27 as a percentage" is by using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 21 (the number we're considering)
- Whole: 27 (the total number)
Let's plug the values into the formula:
(21 / 27) * 100% = ?
-
Divide the part by the whole: 21 divided by 27 is approximately 0.7778
-
Multiply by 100: 0.7778 multiplied by 100 is 77.78
Therefore, 21 out of 27 is 77.78%.
Method 2: Using Proportions
Another way to approach this calculation is by using proportions. We can set up a proportion where 'x' represents the percentage we want to find:
21/27 = x/100
To solve for 'x', we can cross-multiply:
21 * 100 = 27 * x
2100 = 27x
x = 2100 / 27
x ≈ 77.78
Again, this method confirms that 21 out of 27 is approximately 77.78%.
Method 3: Simplifying the Fraction
Before applying the percentage formula, we can simplify the fraction 21/27. Both 21 and 27 are divisible by 3:
21 ÷ 3 = 7 27 ÷ 3 = 9
This simplifies the fraction to 7/9. Now, we can apply the percentage formula:
(7/9) * 100% ≈ 77.78%
Rounding and Accuracy
Note that in all the methods above, we obtained an approximate value of 77.78%. The exact value is a repeating decimal (77.777...). The level of rounding depends on the context. For most practical purposes, rounding to two decimal places (77.78%) is sufficient. However, in situations requiring high precision, you might choose to use more decimal places or represent the answer as a fraction (7/9).
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous situations:
1. Academic Performance:
-
Grade Calculation: Many grading systems use percentages to represent a student's performance on tests, assignments, and overall course grades. Understanding percentages allows students to track their progress and identify areas for improvement.
-
Test Scores: Converting raw scores on standardized tests to percentages provides a standardized measure of achievement, enabling comparisons across different tests and students.
2. Financial Management:
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Calculating percentages is crucial for understanding the cost of borrowing or the return on investment.
-
Discounts and Sales Tax: Businesses use percentages to calculate discounts during sales and to determine sales tax amounts. Consumers need to understand percentages to determine the final price of goods and services.
3. Data Analysis and Interpretation:
-
Statistical Analysis: Percentages are fundamental in statistical analysis for presenting data in a clear and concise manner. For example, survey results are often expressed as percentages to represent the proportion of respondents who chose a specific option.
-
Market Research: Market researchers use percentages to represent market shares, customer satisfaction rates, and other key performance indicators.
-
Data Visualization: Charts and graphs frequently use percentages to visually represent data and highlight trends.
4. Everyday Life:
-
Tip Calculation: Calculating tips in restaurants often involves determining a percentage of the bill amount.
-
Recipe Scaling: Adjusting ingredient quantities in recipes involves using percentages to maintain the correct proportions.
Beyond the Calculation: Interpreting the Result
Calculating that 21 out of 27 is 77.78% is just the first step. Understanding the significance of this percentage within the given context is crucial. For example:
-
Test Score: A score of 77.78% on a test might be considered a passing grade, but its meaning depends on the grading scale and the difficulty of the test.
-
Sales Performance: 77.78% of sales targets achieved could indicate good performance, but it might also highlight areas for improvement depending on the overall business goals.
Therefore, always consider the context of the percentage calculation and interpret the result accordingly.
Conclusion
Calculating "21 out of 27 as a percentage" highlights the importance of understanding percentage calculations in various real-world scenarios. The methods discussed—using the formula, proportions, and simplifying fractions—all yield the same approximate result: 77.78%. Remember that the accuracy required for rounding depends on the context. More importantly, understanding how to interpret the resulting percentage within its specific context is crucial for effective decision-making and data analysis. Mastering percentage calculations is an essential skill that enhances your ability to comprehend and navigate numerical information effectively.
Latest Posts
Latest Posts
-
How Many More Hours Till 7 Am
May 24, 2025
-
How Many Hours Is 8pm To 8am
May 24, 2025
-
What Is 2 Divided By 7
May 24, 2025
-
15 Months Is How Many Days
May 24, 2025
-
Greatest Common Factor For 12 And 16
May 24, 2025
Related Post
Thank you for visiting our website which covers about 21 Out Of 27 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.