2000 Is What Percent Of 5000
listenit
May 23, 2025 · 5 min read
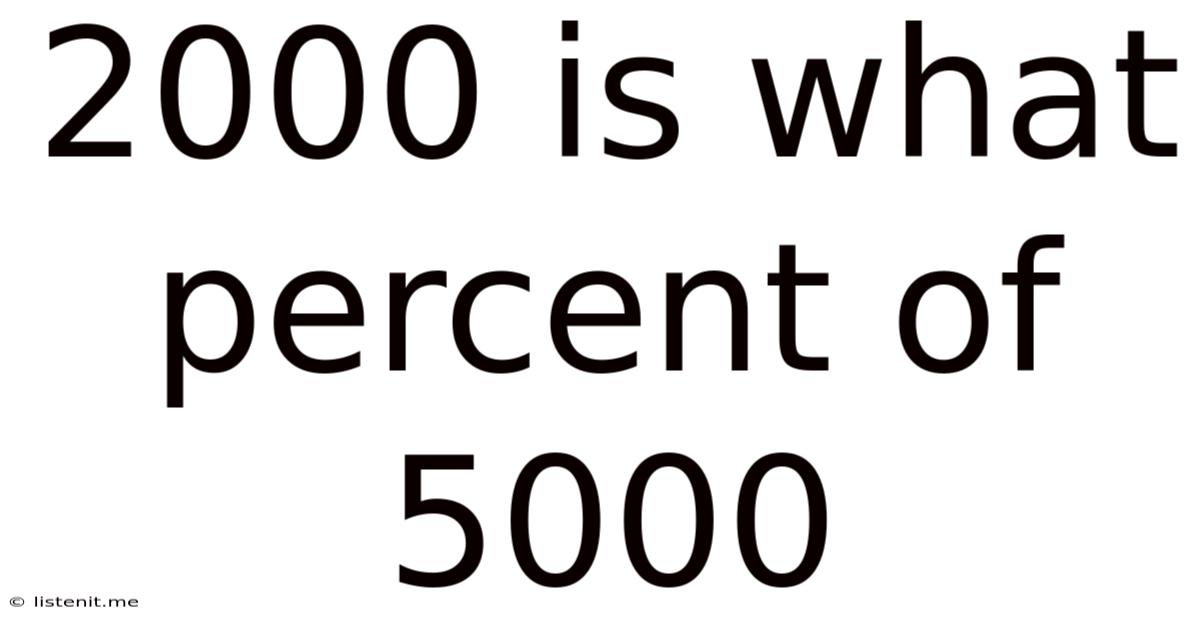
Table of Contents
2000 is What Percent of 5000? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article delves into the question, "2000 is what percent of 5000?", providing a detailed explanation of the calculation process and exploring related percentage concepts. We’ll cover the core calculation, explore different approaches, discuss practical applications, and even touch upon advanced percentage problems.
Understanding the Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Percentages are used extensively to represent proportions, rates, and changes in various contexts.
Calculating "2000 is What Percent of 5000?"
The most straightforward way to solve this is using a simple formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 2000
- Whole: 5000
Substituting these values into the formula:
(2000 / 5000) x 100% = 40%
Therefore, 2000 is 40% of 5000.
Alternative Calculation Methods
While the above method is the most common, there are other approaches you can use to arrive at the same answer:
-
Using Proportions: You can set up a proportion: 2000/5000 = x/100. Solving for x (the percentage) will give you 40.
-
Decimal Conversion: First, divide 2000 by 5000 to get a decimal: 2000/5000 = 0.4. Then, multiply the decimal by 100% to convert it to a percentage: 0.4 x 100% = 40%.
-
Mental Math (for simpler percentages): Recognizing that 2000 is half of 4000, and 4000 is 80% of 5000, you could deduce that 2000 is 40% of 5000. This method works best for percentages easily visualized.
Practical Applications of Percentage Calculations
The ability to calculate percentages has wide-ranging applications in everyday life and various professional fields. Here are some examples:
-
Finance: Calculating interest rates, loan repayments, discounts, and tax amounts all involve percentage calculations. Understanding percentage changes is crucial for tracking investment performance and analyzing financial statements. For example, if your investment of 5000 increases to 7000, you can calculate the percentage increase using the same formula.
-
Retail: Retailers use percentages to calculate discounts (e.g., a 20% off sale), markups (adding a percentage to the cost price to determine the selling price), and sales tax. Consumers need percentage skills to compare prices and understand the actual cost of goods.
-
Data Analysis: Percentages are vital in presenting and interpreting statistical data. They are used to express proportions, rates of change, and relationships between different data sets. Graphs and charts often rely on percentages to illustrate trends and insights. For example, determining the percentage of survey respondents who favor a particular product.
-
Science: In scientific research, percentages are used to express concentrations, yields, and error rates. They are fundamental in many calculations and data representations across various scientific disciplines.
-
Education: Percentages are used to calculate grades, assess student performance, and track progress. Understanding percentages is important for students to grasp academic achievements.
Advanced Percentage Problems and Concepts
Beyond the basic percentage calculation, understanding more complex concepts can be invaluable:
-
Percentage Increase/Decrease: Calculating the percentage change between two numbers involves finding the difference between the numbers, dividing by the original number, and multiplying by 100%. For example, if a price increases from 2000 to 2500, the percentage increase is ((2500-2000)/2000) x 100% = 25%.
-
Compound Interest: Compound interest is interest calculated on the initial principal and also on the accumulated interest from previous periods. Understanding this concept is critical for managing investments and loans.
-
Percentage Points vs. Percentages: It's important to distinguish between percentage points and percentages. A change of 10 percentage points means a direct addition or subtraction of 10 to the percentage. A 10% increase from 20% results in 22%, but a 10 percentage point increase from 20% results in 30%.
-
Finding the Original Value: If you know the percentage and the resulting value, you can work backward to find the original value. For example, if 40% of a number is 2000, the original number is 2000 / 0.4 = 5000.
-
Multiple Percentage Changes: Calculating the effect of multiple percentage changes sequentially is more complex than simply adding the percentages. Each percentage change is applied to the result of the previous change.
Troubleshooting Common Percentage Calculation Mistakes
Several common errors can occur when calculating percentages:
-
Incorrect Formula: Using the wrong formula can lead to inaccurate results. Always double-check your formula before performing the calculation.
-
Decimal Errors: Mistakes in decimal point placement are frequent. Pay close attention to decimal points when performing calculations.
-
Mixing Up Part and Whole: Ensure you are using the correct values for the part and the whole in the formula.
-
Rounding Errors: Rounding off numbers during intermediate steps can introduce inaccuracies into the final result. Avoid rounding until the final answer.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a valuable life skill applicable across many domains. By understanding the fundamental formula, exploring different calculation methods, and practicing with diverse applications, you can develop confidence and proficiency in this crucial mathematical skill. Whether dealing with financial matters, analyzing data, or simply understanding everyday scenarios, a solid grasp of percentages empowers you to make informed decisions and interpret information effectively. This article has provided a comprehensive overview, but continued practice and exploration of advanced concepts will solidify your understanding and broaden your problem-solving capabilities. Remember to always double-check your work and consider the context of the problem to ensure accuracy and meaningful interpretations.
Latest Posts
Latest Posts
-
1 5 Divided By 3 In Fraction Form
May 23, 2025
-
What Is The Percentage Of 6 Out Of 20
May 23, 2025
-
What Is 15 Percent Of 85
May 23, 2025
-
What Is 4 Divided By 12
May 23, 2025
-
What Day Is 15 Days From Today
May 23, 2025
Related Post
Thank you for visiting our website which covers about 2000 Is What Percent Of 5000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.