20 Out Of 60 As A Percentage
listenit
May 24, 2025 · 5 min read
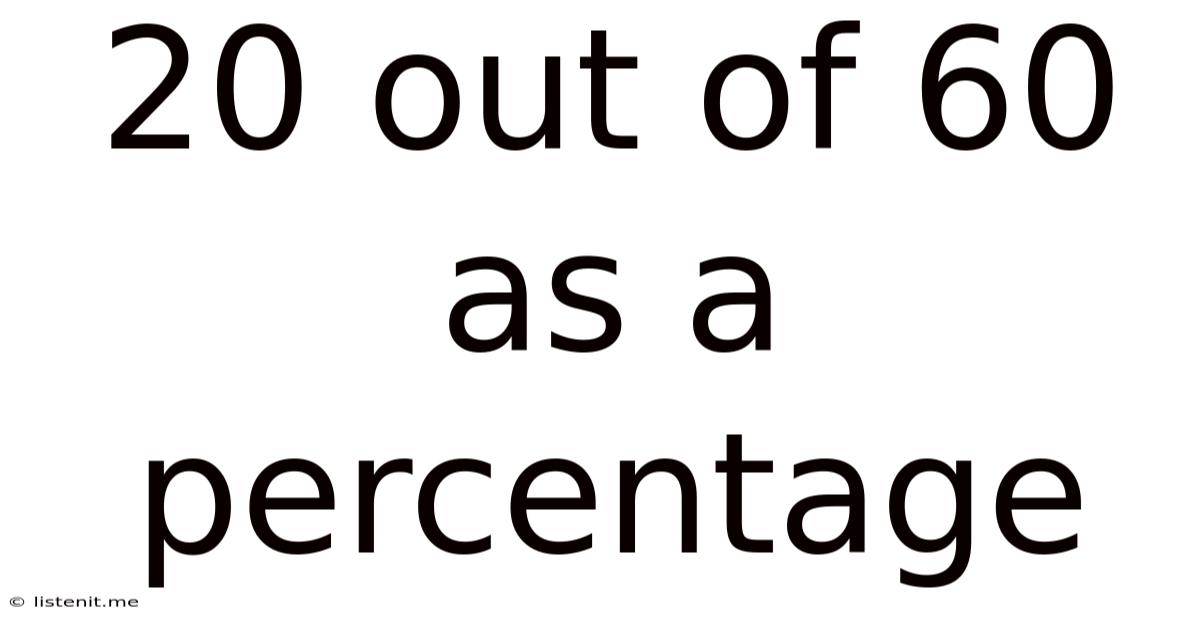
Table of Contents
20 out of 60 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex scientific analyses. Understanding how to determine a percentage, particularly in scenarios like "20 out of 60," is crucial for interpreting data and making informed decisions. This comprehensive guide will not only show you how to calculate 20 out of 60 as a percentage but also explore the broader context of percentage calculations, providing you with a robust understanding of this essential mathematical concept.
Understanding Percentages
Before diving into the specific calculation of 20 out of 60, let's establish a solid foundation in understanding percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to represent percentages. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
The fundamental formula for calculating a percentage is:
(Part / Whole) * 100% = Percentage
Where:
- Part: Represents the specific portion you are interested in.
- Whole: Represents the total amount.
This formula provides a simple yet powerful tool for converting ratios into percentages, making comparisons and interpretations much easier.
Calculating 20 out of 60 as a Percentage
Now, let's apply this formula to the question at hand: What is 20 out of 60 as a percentage?
-
Identify the Part and the Whole: In this case, the part is 20, and the whole is 60.
-
Apply the Formula: Substitute these values into the percentage formula:
(20 / 60) * 100% = Percentage
-
Perform the Calculation: First, divide 20 by 60:
20 / 60 = 0.3333... (This is a recurring decimal)
-
Multiply by 100%:
0.3333... * 100% = 33.33...%
-
Round to Desired Precision: Depending on the context, you might round the percentage to a specific number of decimal places. Rounding to two decimal places, we get:
33.33%
Therefore, 20 out of 60 is equal to 33.33%.
Practical Applications and Real-World Examples
Understanding percentage calculations is vital in numerous real-world scenarios. Here are some examples showcasing the practical application of this skill:
1. Academic Performance:
Imagine a student scoring 20 out of 60 marks on a test. Converting this score to a percentage (33.33%) provides a clearer understanding of their performance relative to the total possible marks. This allows for easier comparison with other students and assessment of their progress.
2. Sales and Marketing:
Businesses use percentages extensively to track sales figures, conversion rates, and marketing campaign success. For example, if a company aims to sell 60 units of a product and manages to sell 20, their sales performance can be represented as 33.33%. This data informs future strategies and resource allocation.
3. Financial Analysis:
In finance, percentages are crucial for analyzing investment returns, calculating interest rates, and evaluating financial performance. Understanding percentage changes in stock prices, interest accrual, or debt levels is essential for informed financial decision-making.
4. Surveys and Statistics:
Surveys and statistical analysis frequently employ percentages to represent proportions of a population holding a particular view or exhibiting a certain characteristic. For instance, if 20 out of 60 respondents in a survey prefer a particular brand, this represents a 33.33% preference.
5. Everyday Budgeting:
Percentages help in budgeting and managing personal finances. For example, determining what percentage of your monthly income is allocated to different expenses (rent, food, transportation) allows for effective resource management and financial planning.
Beyond the Basics: Further Exploration of Percentage Calculations
While calculating 20 out of 60 as a percentage is relatively straightforward, understanding more complex percentage calculations can be highly beneficial. Here are some extensions of the basic concept:
1. Calculating Percentage Increase or Decrease:
This involves determining the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100%
For example, if sales increased from 40 units to 60 units, the percentage increase would be:
[(60 - 40) / 40] * 100% = 50%
2. Finding the Whole when the Percentage and Part are Known:
Sometimes, you might know the percentage and the part but need to find the whole. The formula for this is:
Whole = (Part / Percentage) * 100
For example, if 33.33% of a number is 20, the whole number would be:
(20 / 33.33) * 100 ≈ 60
3. Calculating Percentage Points:
Percentage points refer to the difference between two percentages, not the percentage change. For example, if a company's market share increased from 20% to 33.33%, the increase is 13.33 percentage points, not 13.33%.
4. Working with Compound Percentages:
Compound percentages involve applying a percentage change to a value multiple times. This is commonly seen in compound interest calculations where interest earned is added to the principal amount, and subsequent interest is calculated on the new total.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill with wide-ranging applications across diverse fields. By understanding the fundamental formula and its various applications, you can confidently tackle various percentage-related problems, whether it's determining the percentage representation of a specific ratio, like "20 out of 60," or engaging with more complex percentage calculations involving increases, decreases, or compound effects. This guide provides a solid foundation for enhancing your mathematical proficiency and making informed decisions in numerous real-world situations. Remember to practice regularly to solidify your understanding and build confidence in applying these principles effectively. Consistent practice will transform these concepts from abstract ideas into practical tools you can use every day.
Latest Posts
Latest Posts
-
How Much Is Rent For A 5 Million Dollar House
May 24, 2025
-
Born 1962 How Old Am I
May 24, 2025
-
Find The Greatest Common Factor Of 16 And 9
May 24, 2025
-
Metal Roof Cost Per Square Foot Calculator
May 24, 2025
-
What Is The Area Of The Shape Below
May 24, 2025
Related Post
Thank you for visiting our website which covers about 20 Out Of 60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.