2 X 8 Solve For X
listenit
May 10, 2025 · 4 min read
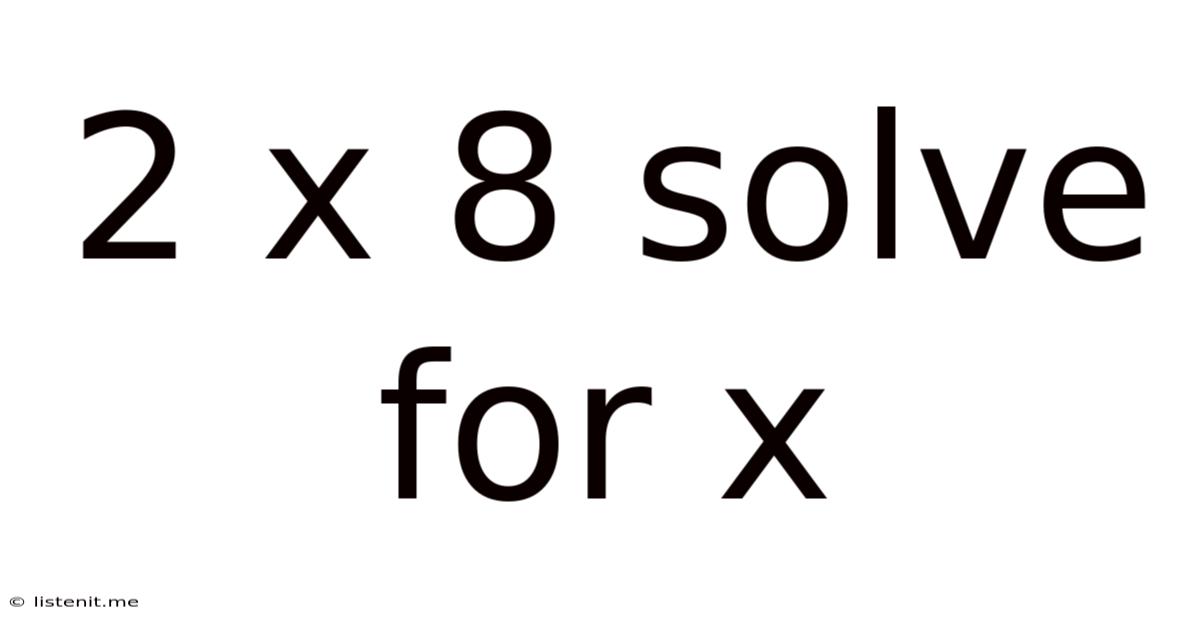
Table of Contents
Solving for x: A Comprehensive Guide to 2x + 8 = 0 and its Variations
This article provides a thorough explanation of how to solve the equation 2x + 8 = 0, covering the fundamental algebraic principles involved. We'll explore various approaches, address common mistakes, and expand upon the concept to encompass similar equations. Understanding this seemingly simple equation is crucial for building a solid foundation in algebra and solving more complex problems.
Understanding the Equation: 2x + 8 = 0
The equation 2x + 8 = 0 represents a linear equation in one variable, 'x'. Our goal is to isolate 'x' on one side of the equation to find its value. This involves applying fundamental algebraic operations. The equation states that twice a number (2x) plus eight (8) equals zero (0).
Key Concepts:
- Variable (x): An unknown quantity we aim to determine.
- Coefficient (2): The number multiplying the variable.
- Constant (8): A fixed numerical value.
- Equation: A mathematical statement showing the equality of two expressions.
Solving 2x + 8 = 0: Step-by-Step Solution
We solve this equation by employing inverse operations to isolate 'x'. The steps are as follows:
-
Subtract 8 from both sides: This eliminates the constant term from the left side.
2x + 8 - 8 = 0 - 8
This simplifies to:
2x = -8
-
Divide both sides by 2: This isolates 'x' by canceling out its coefficient.
2x / 2 = -8 / 2
This gives us the solution:
x = -4
Therefore, the solution to the equation 2x + 8 = 0 is x = -4.
Verification: Checking the Solution
To ensure our solution is correct, we substitute x = -4 back into the original equation:
2(-4) + 8 = 0
-8 + 8 = 0
0 = 0
Since the equation holds true, our solution x = -4 is verified.
Expanding the Concept: Solving Similar Equations
The process for solving 2x + 8 = 0 can be generalized to solve a broad range of linear equations. Let's examine similar equations and how to tackle them:
Equation Type 1: ax + b = c
This represents a general form of linear equations where 'a', 'b', and 'c' are constants. The solution follows these steps:
- Subtract 'b' from both sides: ax + b - b = c - b => ax = c - b
- Divide both sides by 'a': ax / a = (c - b) / a => x = (c - b) / a
Example: Solve 3x + 5 = 11
- Subtract 5 from both sides: 3x = 6
- Divide both sides by 3: x = 2
Equation Type 2: Equations with Fractions
Equations involving fractions can be solved by first eliminating the fractions. This is usually done by finding the least common denominator (LCD) and multiplying both sides of the equation by it.
Example: Solve (1/2)x + 3 = 7
- Subtract 3 from both sides: (1/2)x = 4
- Multiply both sides by 2: x = 8
Equation Type 3: Equations with Parentheses
Equations with parentheses require simplifying the expression within the parentheses first, usually using the distributive property (a(b + c) = ab + ac).
Example: Solve 2(x + 3) = 10
- Distribute the 2: 2x + 6 = 10
- Subtract 6 from both sides: 2x = 4
- Divide both sides by 2: x = 2
Equation Type 4: Equations with Decimals
Equations involving decimals can be simplified by multiplying both sides of the equation by a power of 10 to eliminate the decimal points.
Example: Solve 0.5x + 1.5 = 3.5
- Multiply both sides by 10: 5x + 15 = 35
- Subtract 15 from both sides: 5x = 20
- Divide both sides by 5: x = 4
Common Mistakes to Avoid
Several common mistakes can hinder accurate problem-solving:
- Incorrect Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) consistently.
- Errors in Sign Changes: Pay close attention to signs when adding, subtracting, multiplying, or dividing. A simple sign error can lead to an incorrect result.
- Forgetting to Apply Operations to Both Sides: Always perform the same operation on both sides of the equation to maintain balance.
- Division by Zero: Avoid division by zero, as it's undefined.
Beyond the Basics: Applications of Linear Equations
Linear equations like 2x + 8 = 0 have far-reaching applications in various fields:
- Physics: Modeling motion, calculating forces, and analyzing electrical circuits.
- Engineering: Designing structures, analyzing stress and strain, and controlling systems.
- Economics: Predicting market trends, analyzing supply and demand, and modeling economic growth.
- Computer Science: Developing algorithms, creating simulations, and managing data.
Understanding how to solve these equations is a foundational step in applying mathematical concepts to real-world problems.
Conclusion: Mastering the Fundamentals
Solving the equation 2x + 8 = 0, and variations thereof, is a fundamental skill in algebra. By understanding the principles of inverse operations and consistently applying them, you can confidently solve a wide range of linear equations. Mastering this skill is essential for further mathematical studies and numerous real-world applications. Remember to practice regularly, pay attention to detail, and always check your solutions to reinforce your understanding. Through diligent practice and a keen eye for detail, you will confidently navigate the world of algebraic equations.
Latest Posts
Latest Posts
-
Classify These Structures By The Hybridization Of The Central Atom
May 11, 2025
-
10 Out Of 200 As A Percentage
May 11, 2025
-
Does Earth Rotate West To East
May 11, 2025
-
Rewrite Each Fraction Using The Given Denominator
May 11, 2025
-
What Is The Gcf Of 63 And 42
May 11, 2025
Related Post
Thank you for visiting our website which covers about 2 X 8 Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.