2 X 2 X 2 X 2 X
listenit
Jun 14, 2025 · 5 min read
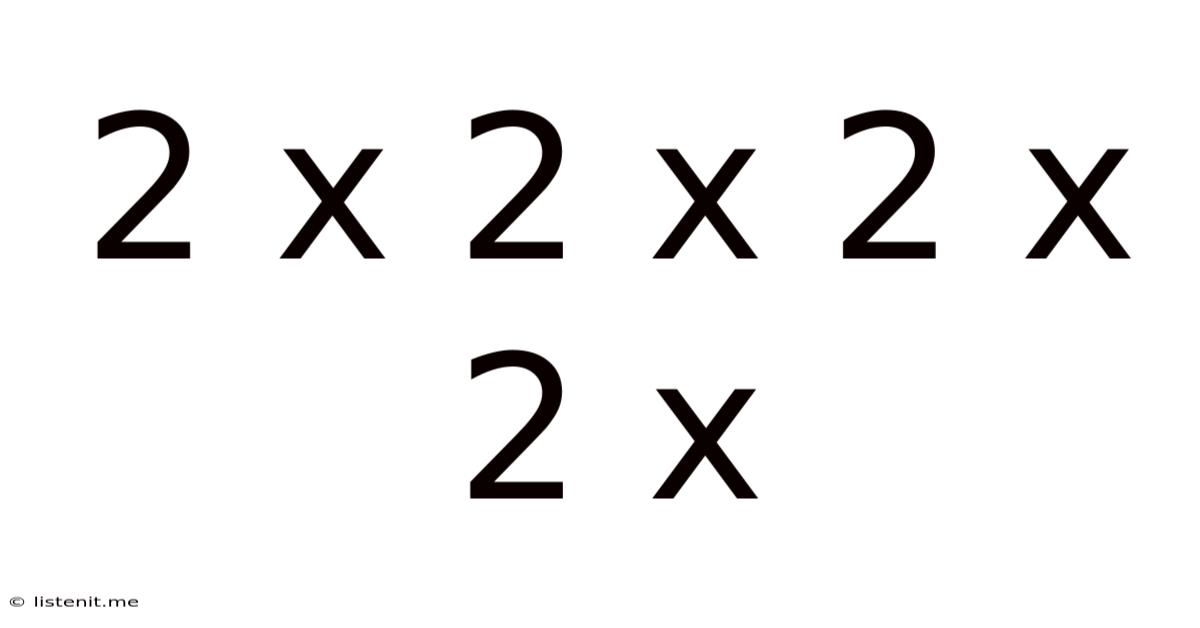
Table of Contents
Decoding the Mystery: Exploring the Mathematical and Conceptual Significance of 2 x 2 x 2 x 2 x
The seemingly simple expression "2 x 2 x 2 x 2 x" sparks curiosity. While the missing final number leaves it incomplete, the core concept of repeated multiplication opens doors to a fascinating exploration of mathematics, computer science, and even philosophy. This article delves into the various interpretations and implications of this repeated multiplication, examining its mathematical properties, its relevance in computational processes, and its broader significance in understanding patterns and growth.
The Fundamental Arithmetic: Powers of Two
At its most basic level, "2 x 2 x 2 x 2 x" represents a power of two. If we assume the missing number is also 2, we have 2<sup>5</sup>, which equals 32. Understanding powers of two is fundamental in numerous fields.
-
Binary System: The backbone of modern computing is the binary system, which uses only two digits (0 and 1). Powers of two are crucial for representing numbers in binary, understanding memory allocation (kilobytes, megabytes, gigabytes, etc.), and processing data. Each bit represents a power of two (2<sup>0</sup>, 2<sup>1</sup>, 2<sup>2</sup>, and so on).
-
Exponential Growth: Powers of two exemplify exponential growth, a concept applicable in numerous real-world scenarios. Consider population growth (under ideal conditions), compound interest, or the spread of viral information. The rapid increase characteristic of exponential growth is visually represented by the increasing values of successive powers of two.
-
Geometric Progression: The sequence formed by powers of two (1, 2, 4, 8, 16, 32,...) is a geometric progression. A geometric progression is a sequence where each term is the product of the previous term and a constant value (in this case, 2). This type of sequence is often used to model growth and decay phenomena in various scientific and financial contexts.
Beyond the Simple Calculation: Exploring the Missing Factor
The incomplete nature of "2 x 2 x 2 x 2 x" invites us to consider the possibilities. The missing factor could be any number, leading to a range of results and applications.
-
Variable Representation: In mathematics, we can represent the missing factor using a variable, such as 'x'. The expression becomes 32x. This introduces algebraic manipulation, allowing us to solve for 'x' given certain conditions or to explore how the final result changes based on different values of 'x'.
-
Functional Relationships: We can consider the incomplete expression as a function, f(x) = 32x. This allows us to explore the relationship between the input (x) and the output (32x). We can analyze the function's properties: its domain, range, and behavior as x approaches different values (including infinity and negative infinity).
-
Iterative Processes: In computer science, the repetitive nature of "2 x 2 x 2 x 2 x" might be part of an iterative process. The expression might represent a loop that multiplies a variable by 2 several times. Understanding this iterative aspect is crucial for designing algorithms and optimizing computational efficiency.
Implications in Different Fields:
The repeated multiplication of 2, even in its incomplete form, has profound implications across various disciplines.
-
Computer Science and Data Structures: As previously mentioned, powers of two are fundamental in computer science. Data structures like binary trees and heaps rely on the properties of powers of two for efficient organization and retrieval of data. The concept of bit manipulation and binary arithmetic directly relates to the understanding of powers of two. The efficiency of algorithms designed to operate on binary data often depends heavily on the properties of powers of two.
-
Physics and Engineering: Exponential growth and decay, often modeled using powers of 2 or related functions, appear in many physical phenomena. Radioactive decay, the charging and discharging of capacitors, and certain aspects of wave propagation involve exponential functions.
-
Biology and Genetics: Cellular growth and division often exhibit exponential patterns, mirroring the behavior of powers of two. Understanding these patterns is critical in modeling population dynamics and understanding biological processes.
-
Finance and Economics: Compound interest, a cornerstone of financial modeling, relies on exponential growth. Understanding how powers of two relate to compound interest allows for accurate projections of investment returns and debt accumulation.
Beyond the Numbers: Exploring the Conceptual Significance
Moving beyond the specific mathematical calculations, the expression "2 x 2 x 2 x 2 x" can spark deeper philosophical and conceptual inquiries.
-
Patterns and Repetition: The expression highlights the power of pattern recognition and the significance of repetition in mathematics and nature. Many natural phenomena exhibit patterns that can be expressed using mathematical models, including those involving powers of two or similar repetitive structures.
-
Growth and Complexity: The repeated multiplication demonstrates how simple operations can lead to rapid growth and increasing complexity. This mirrors the way small changes or innovations can have a significant cumulative effect over time.
-
The Unknown Factor: The missing 'x' introduces uncertainty and the need for further investigation. In many real-world problems, we face incomplete information, requiring us to employ various techniques to estimate, analyze, and model the situation.
Advanced Concepts and Further Exploration:
For those interested in delving deeper, the following concepts build upon the fundamental ideas presented:
-
Limits and Calculus: Exploring the behavior of the expression as 'x' approaches infinity or zero using calculus provides a more comprehensive understanding of the function f(x) = 32x.
-
Series and Sequences: Analyzing the infinite series generated by repeatedly multiplying by 2 and exploring its convergence properties leads to advanced mathematical concepts.
-
Number Theory: Exploring the properties of powers of two within the broader context of number theory reveals connections to prime numbers, modular arithmetic, and other advanced topics.
-
Complex Numbers: Extending the analysis to include complex numbers opens up new dimensions in mathematical exploration.
Conclusion:
The seemingly simple expression "2 x 2 x 2 x 2 x" reveals a wealth of mathematical and conceptual richness. From its fundamental role in computer science and its applications in various scientific fields to its broader implications for understanding growth, patterns, and complexity, this expression offers a fascinating entry point into many branches of mathematics and beyond. The missing factor, represented by 'x', invites further exploration and emphasizes the importance of considering variables and uncertainty in mathematical modeling. By exploring its various interpretations and implications, we gain a deeper appreciation for the power of repeated multiplication and its fundamental significance in our understanding of the world around us. The simplicity of the expression belies its profound depth, highlighting the beauty and power of mathematical thinking.
Latest Posts
Latest Posts
-
How To Remove Paint Off Tiles
Jun 15, 2025
-
How To Tell If Wood Is Pressure Treated
Jun 15, 2025
-
What Color Is The Opposite Of Yellow
Jun 15, 2025
-
How To Stop Cat From Peeing On Rug
Jun 15, 2025
-
Thanks To The Both Of You
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 X 2 X 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.