2 Out Of 30 Is What Percent
listenit
May 25, 2025 · 5 min read
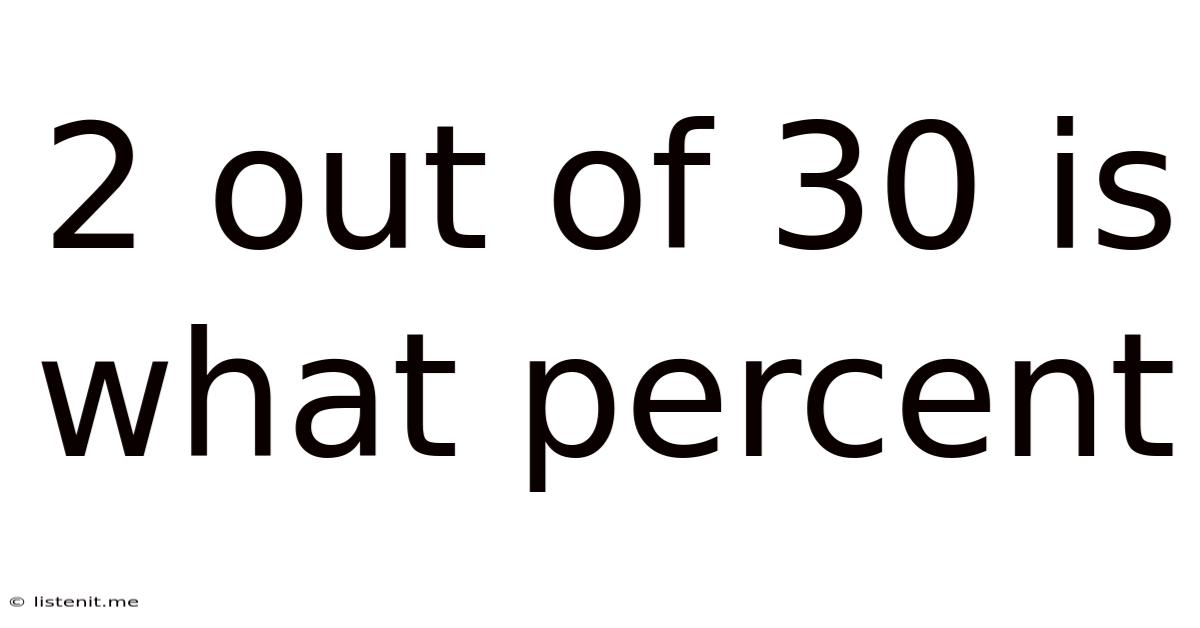
Table of Contents
2 Out of 30 is What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to comprehending statistical data and analyzing financial reports. This comprehensive guide will not only answer the question, "2 out of 30 is what percent?" but will also equip you with the knowledge and tools to tackle similar percentage problems with confidence. We'll explore different methods of calculation, delve into the underlying principles, and provide practical examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4.
Method 1: Using the Basic Percentage Formula
The most straightforward method to determine what percentage 2 out of 30 represents is to use the fundamental percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 2 (the number we're considering as a part of the whole)
- Whole: 30 (the total number)
Let's plug these values into the formula:
(2 / 30) x 100 = 6.67% (approximately)
Therefore, 2 out of 30 is approximately 6.67%.
Method 2: Simplifying the Fraction
Before applying the percentage formula, we can simplify the fraction 2/30. Both the numerator (2) and the denominator (30) are divisible by 2:
2/30 simplifies to 1/15
Now, we can use the percentage formula with the simplified fraction:
(1 / 15) x 100 ≈ 6.67%
This method demonstrates that simplifying the fraction before calculating the percentage can sometimes make the calculation easier.
Method 3: Using Decimal Conversion
Another approach involves converting the fraction to a decimal first and then multiplying by 100:
2/30 = 0.066666...
Multiplying the decimal by 100:
0.066666... x 100 ≈ 6.67%
This method highlights the direct relationship between decimals and percentages. Moving the decimal point two places to the right is equivalent to multiplying by 100.
Practical Applications: Real-World Examples
The ability to calculate percentages is crucial in numerous real-world scenarios. Here are a few examples showcasing the practical applications of understanding "2 out of 30 is what percent?":
-
Test Scores: If you answered 2 questions correctly out of 30 on a test, your score would be approximately 6.67%. This allows you to assess your performance and identify areas for improvement.
-
Sales Conversions: In sales, if 2 out of 30 potential customers made a purchase, your conversion rate is about 6.67%. This metric helps businesses analyze their marketing strategies and optimize their sales processes.
-
Survey Results: If 2 out of 30 respondents answered "yes" to a particular question in a survey, the percentage of "yes" responses would be around 6.67%. This data provides insights into public opinion or customer preferences.
-
Quality Control: In manufacturing, if 2 out of 30 products are found to be defective, the defect rate is approximately 6.67%. This helps manufacturers identify and address quality control issues.
-
Financial Analysis: If you invest in a portfolio and two out of thirty stocks yielded significant gains, you can calculate the percentage of successful stocks in your portfolio. This will help in further investment strategies.
Beyond the Basics: Working with Larger Numbers and More Complex Scenarios
While the example of 2 out of 30 is relatively simple, the principles discussed can be applied to more complex percentage calculations involving larger numbers or more intricate scenarios. For instance:
-
Calculating Percentages of Percentages: Imagine you have a 10% discount on an item already reduced by 20%. You would need to calculate the percentage based on the already discounted price.
-
Compound Interest: Calculating compound interest involves repeated percentage calculations over time. Understanding the fundamental concepts of percentages is crucial for grasping the mechanics of compound interest.
-
Statistical Analysis: Percentages are fundamental to statistical analysis, such as calculating probabilities, proportions, and ratios within datasets.
-
Data Visualization: Percentages are frequently used in charts and graphs to represent data visually, making it easier to understand and interpret.
Mastering Percentage Calculations: Tips and Tricks
Here are some tips and tricks to enhance your percentage calculation skills:
-
Practice Regularly: The more you practice, the more confident and proficient you'll become.
-
Use a Calculator: For more complex calculations, using a calculator can save time and reduce the risk of errors. Many calculators have a percentage function that simplifies the process.
-
Learn Mental Math Shortcuts: Developing mental math skills for simple percentage calculations can be incredibly useful in everyday life. For example, 10% of a number is simply moving the decimal point one place to the left.
-
Understand the Relationship Between Fractions, Decimals, and Percentages: A strong grasp of the interconnections between these three representations will significantly improve your ability to solve percentage problems.
-
Break Down Complex Problems: If faced with a complex percentage problem, break it down into smaller, more manageable steps.
Conclusion: The Power of Percentage Understanding
Understanding how to calculate percentages is a valuable skill with wide-ranging applications in various fields. This article has demonstrated multiple methods for determining what percentage 2 out of 30 represents, emphasizing the fundamental formula and exploring alternative approaches. By mastering percentage calculations, you'll not only be able to solve specific problems like "2 out of 30 is what percent?" but also gain a deeper understanding of numerical relationships and improve your analytical skills across a variety of contexts. Remember to practice regularly and explore different methods to find the approach that suits you best. With consistent practice and a clear understanding of the underlying principles, you'll confidently navigate the world of percentages and unlock their practical potential.
Latest Posts
Latest Posts
-
1200 Btu Air Conditioner Room Size
May 26, 2025
-
Write 8 4 5 As A Decimal Number
May 26, 2025
-
How Many Square Feet Is 30x50
May 26, 2025
-
10 To The Power Of 93
May 26, 2025
-
What Is An Hour And 40 Minutes From Now
May 26, 2025
Related Post
Thank you for visiting our website which covers about 2 Out Of 30 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.