2 8 18 32 18 1
listenit
May 11, 2025 · 5 min read
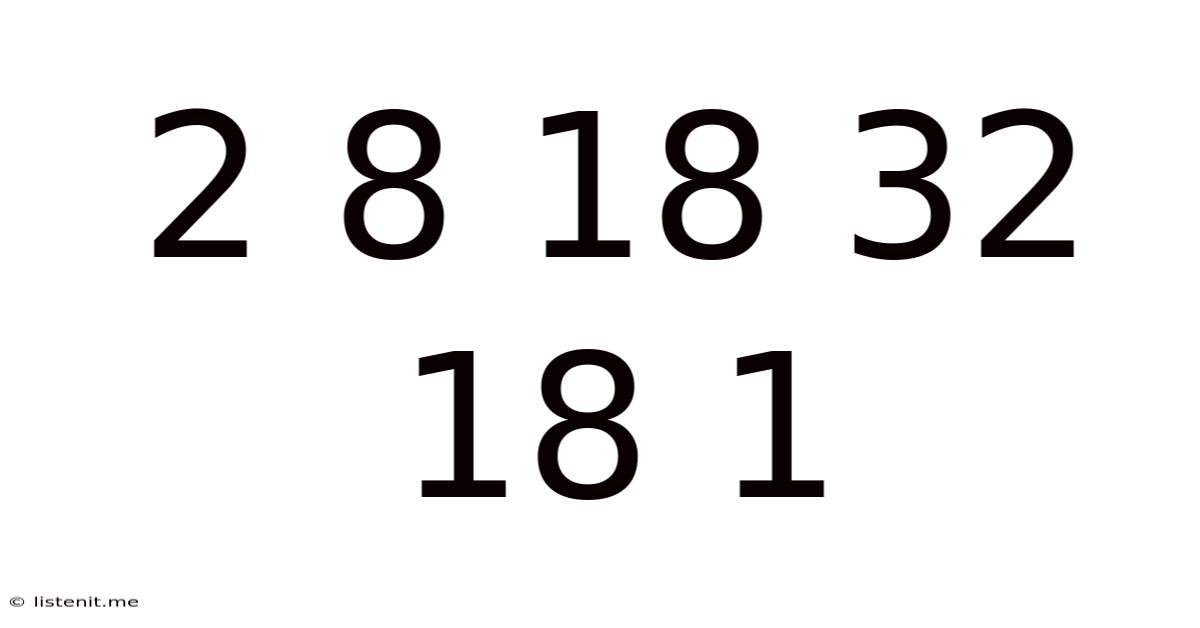
Table of Contents
Decoding the Sequence: 2 8 18 32 18 1 – A Deep Dive into Pattern Recognition and Number Theory
The seemingly innocuous sequence – 2, 8, 18, 32, 18, 1 – presents a captivating challenge for those interested in pattern recognition and number theory. At first glance, it appears random, but a closer examination reveals underlying structures and potential mathematical relationships. This article will explore various approaches to understanding this sequence, delving into different mathematical concepts and methodologies to uncover its hidden logic. We will consider possibilities such as finite differences, polynomial fits, recursive relationships, and even more abstract mathematical structures. Our aim is to not just find a solution, but to explore multiple potential interpretations, highlighting the multifaceted nature of mathematical problem-solving.
Analyzing the Differences: A Finite Difference Approach
A common strategy in sequence analysis is to examine the differences between consecutive terms. Let's apply this method to our sequence:
- First Differences: 6, 10, 14, -14, -17
- Second Differences: 4, 4, -28, -3
The first differences themselves don't immediately reveal a clear pattern. The second differences are even more erratic. This suggests that a simple linear or quadratic relationship is unlikely. The abrupt change in sign and magnitude in the first and second differences indicates a more complex pattern is at play. This negative jump strongly suggests a non-monotonic function, meaning the sequence does not consistently increase or decrease.
Exploring Polynomial Fits: A Curve Fitting Approach
Another approach is to try fitting a polynomial curve to the data. Since we have six terms, a fifth-degree polynomial could potentially fit the data perfectly. However, this approach, while mathematically possible, often leads to a solution that lacks practical meaning or intuitive interpretation. A higher-degree polynomial might accurately represent the given data points, but it wouldn't necessarily predict future terms reliably or reveal the underlying structure of the sequence. The goal isn't just to fit a curve; it's to find a meaningful mathematical relationship that explains the sequence's generation.
Investigating Recursive Relationships: Self-Referential Patterns
Recursive relationships define a term in the sequence based on previous terms. Let's explore this possibility. It’s difficult to identify a simple recursive pattern directly. The lack of consistent growth or decay makes it challenging to define a clear recursive rule using only addition or subtraction. However, more complex recursive functions involving multiplication, division, or a combination of arithmetic operations might be applicable. A potential approach would involve analyzing the ratios between consecutive terms, or exploring combinations of previous terms that might produce the next term. This could involve multiple layers of recursion, making it computationally more intensive but potentially uncovering a hidden self-referential structure within the sequence.
Considering Modular Arithmetic: Cyclical Patterns
Modular arithmetic examines remainders after division. Let's examine the remainders when the terms are divided by different integers:
- Modulo 2: 0, 0, 0, 0, 0, 1 (This doesn't reveal a strong pattern)
- Modulo 3: 2, 2, 0, 2, 0, 1 (Again, no obvious pattern)
- Modulo 4: 2, 0, 2, 0, 2, 1 (A possible pattern emerges: 2, 0, 2, 0, 2, 1)
- Modulo 5: 2, 3, 3, 2, 3, 1 (No clear pattern)
The modulo 4 operation hints at a potential cyclical pattern, but it's not conclusive. Further investigation with other moduli and different mathematical transformations is needed. This exploration highlights the potential for hidden cyclical patterns within the sequence that might not be immediately apparent.
The Role of Prime Numbers and Factorization: Number Theoretic Approaches
Prime factorization is a powerful tool in number theory. Let's analyze the prime factorization of each term:
- 2 = 2
- 8 = 2³
- 18 = 2 × 3²
- 32 = 2⁵
- 18 = 2 × 3²
- 1 = 1
The prominent presence of the prime number 2 suggests a possible connection. The repeated appearance of 18 (2 × 3²) is also notable. However, the inclusion of 1 breaks the pattern and makes it challenging to define a direct relationship based solely on prime factorization.
Abstract Mathematical Structures: Exploring Beyond Elementary Arithmetic
More advanced mathematical concepts could be involved. For instance, the sequence could be related to coefficients of a polynomial, elements of a specific group or ring in abstract algebra, or even connected to some combinatorial problem. The small number of elements in the sequence makes it difficult to identify any of these more advanced relationships with certainty.
The Importance of Context: The Missing Information
The most crucial element missing is the context. Where did this sequence come from? Is it part of a larger problem? Knowing the origin of the sequence would provide invaluable clues. It could be a segment of a larger, more predictable sequence, part of a puzzle, or a result of a specific mathematical operation. Without context, we can only speculate about its underlying structure. This emphasizes the importance of considering the source and surrounding information when attempting to solve mathematical problems.
Conclusion: The Elusive Pattern
The sequence 2, 8, 18, 32, 18, 1 remains an intriguing puzzle. While simple linear or quadratic relationships are unlikely, several potential avenues for further investigation have been identified. The lack of a clear, readily apparent pattern underscores the complexities of sequence analysis. More information about the context and origin of the sequence is crucial to definitively determine its underlying structure. This exploration, however, demonstrates the value of using multiple approaches – from finite differences to modular arithmetic and prime factorization – when trying to decipher such mathematical enigmas. The sequence serves as a reminder that even seemingly simple patterns can hide profound mathematical depths, and the search for understanding often requires creativity, persistence, and a diverse toolkit of mathematical techniques. The exploration, in itself, provides valuable experience in applying these techniques and honing mathematical reasoning skills. The inherent ambiguity of the problem also highlights the limitations of purely data-driven approaches; the inclusion of context and domain knowledge is key to unlocking the true meaning behind the sequence.
Latest Posts
Latest Posts
-
Find The Slope Of The Line Through P And Q
May 11, 2025
-
In Which Subshells Are The Valence Electrons Found
May 11, 2025
-
Which Of These Is An Example Of Mechanical Digestion
May 11, 2025
-
How To Find A Vector Orthogonal To A Plane
May 11, 2025
-
Give The Systematic Name For The Compound Mg No3 2
May 11, 2025
Related Post
Thank you for visiting our website which covers about 2 8 18 32 18 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.