2 3 Divided By 3 4 As A Fraction
listenit
May 09, 2025 · 5 min read
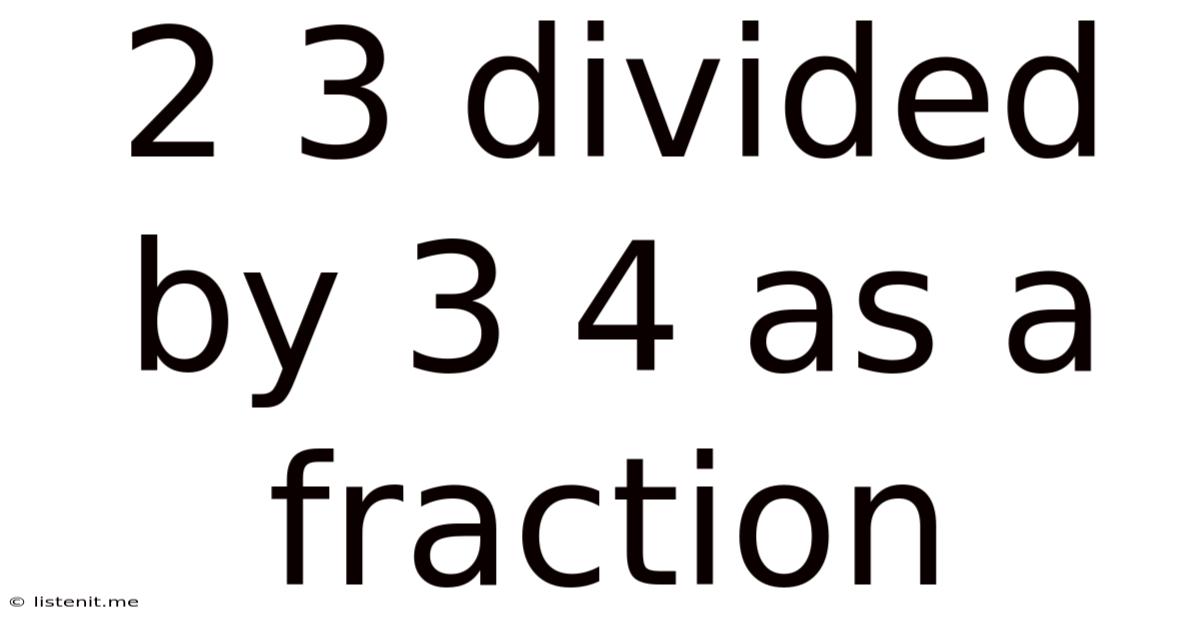
Table of Contents
2/3 Divided by 3/4 as a Fraction: A Comprehensive Guide
Understanding fractions and how to perform operations like division on them is crucial for various mathematical applications. This comprehensive guide delves into the process of dividing fractions, specifically addressing the problem of 2/3 divided by 3/4, exploring the underlying principles, providing step-by-step solutions, and offering practical examples. We'll also touch upon the broader context of fraction division and its relevance in different fields.
Understanding Fraction Division
Before tackling the specific problem, let's solidify our understanding of fraction division. Dividing by a fraction is essentially the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction inverted; the numerator becomes the denominator and vice versa. For example, the reciprocal of 3/4 is 4/3.
Key Concept: Dividing by a fraction is equivalent to multiplying by its reciprocal. This fundamental principle forms the backbone of solving fraction division problems.
Solving 2/3 Divided by 3/4
Now, let's apply this principle to our problem: 2/3 ÷ 3/4.
Step 1: Find the reciprocal of the second fraction.
The second fraction is 3/4. Its reciprocal is 4/3.
Step 2: Change the division operation to multiplication.
Our problem now transforms from 2/3 ÷ 3/4 to 2/3 × 4/3.
Step 3: Multiply the numerators and the denominators.
Multiply the numerators together (2 × 4 = 8) and the denominators together (3 × 3 = 9).
Step 4: Simplify the resulting fraction (if possible).
The result of the multiplication is 8/9. In this case, the fraction is already in its simplest form because 8 and 9 share no common factors other than 1.
Therefore, 2/3 divided by 3/4 is 8/9.
Visualizing Fraction Division
Visual aids can often help to grasp the concept of fraction division more intuitively. Imagine you have 2/3 of a pizza. You want to divide this 2/3 into portions that are each 3/4 the size of the original pizza. How many of these smaller portions will you get? The answer, as we've calculated, is 8/9. This means you'll have slightly less than a whole pizza's worth of smaller portions.
Practical Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it finds applications in many real-world scenarios. Here are a few examples:
-
Baking: Recipes often require dividing ingredients into fractions. If a recipe calls for 2/3 of a cup of flour and you want to make only 3/4 of the recipe, you'll need to calculate (2/3) ÷ (3/4) = 8/9 of a cup of flour.
-
Sewing: Tailors and seamstresses frequently work with fabric measurements involving fractions. Determining how many pieces of a certain length can be cut from a larger piece of fabric involves fraction division.
-
Construction: Measuring and cutting materials in construction projects often necessitates working with fractions. Dividing lengths or areas involves similar calculations.
-
Finance: Financial calculations, such as dividing shares of ownership or calculating portions of a budget, frequently utilize fractions and require division of fractions.
Further Exploring Fraction Operations
Beyond division, understanding other operations with fractions is equally important. Let's briefly explore addition, subtraction, and multiplication.
Adding Fractions:
To add fractions, they must have a common denominator. If they don't, find the least common multiple (LCM) of the denominators and adjust the numerators accordingly. Then, add the numerators and keep the common denominator. For example:
1/2 + 1/4 = (2/4) + (1/4) = 3/4
Subtracting Fractions:
Similar to addition, subtraction of fractions requires a common denominator. Subtract the numerators and keep the common denominator. For example:
3/4 - 1/2 = (3/4) - (2/4) = 1/4
Multiplying Fractions:
Multiplying fractions is straightforward. Multiply the numerators together and the denominators together. Simplify the resulting fraction if possible. For example:
1/2 × 1/4 = 1/8
Advanced Concepts: Complex Fractions and Mixed Numbers
The world of fractions extends beyond simple fractions. We can encounter complex fractions (fractions within fractions) and mixed numbers (a whole number combined with a fraction). Let's briefly discuss how to handle these:
Complex Fractions: To simplify a complex fraction, treat it as a division problem. The numerator becomes the dividend, and the denominator becomes the divisor. Then apply the rules of fraction division.
Mixed Numbers: To perform operations with mixed numbers, it's generally easiest to convert them into improper fractions (where the numerator is larger than the denominator). After performing the operation, convert the result back to a mixed number if needed.
Troubleshooting Common Mistakes in Fraction Division
Even with a clear understanding of the principles, some common mistakes can occur when working with fractions. Here are a few to watch out for:
-
Incorrectly finding the reciprocal: Remember to flip the second fraction (the divisor) to find its reciprocal before multiplying.
-
Forgetting to simplify: Always simplify the resulting fraction to its lowest terms.
-
Errors in arithmetic: Double-check your calculations, especially when working with larger numbers or more complex fractions.
-
Improper handling of mixed numbers: Convert mixed numbers to improper fractions before performing operations.
Conclusion: Mastering Fraction Division
Mastering fraction division is a fundamental skill in mathematics with practical applications in many real-world scenarios. By understanding the core principles, practicing regularly, and being mindful of potential errors, you can confidently tackle fraction division problems of any complexity, including the specific example of 2/3 divided by 3/4, which results in the fraction 8/9. Remember the key takeaway: dividing by a fraction is the same as multiplying by its reciprocal. This simple rule unlocks the door to solving a wide range of fractional calculations. Continual practice and attention to detail will ensure proficiency in this essential area of mathematics.
Latest Posts
Latest Posts
-
Which Is One Of The Lewis Structures For Ozone
May 09, 2025
-
Second Most Abundant Element In Earth Crust
May 09, 2025
-
Which Molecule Has Polar Bonds But Is Non Polar
May 09, 2025
-
What Is The Least Common Multiple Of 3 And 11
May 09, 2025
-
Greatest Common Factor Of 32 And 64
May 09, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 3 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.