2 3 Divided By 2 3
listenit
May 18, 2025 · 5 min read
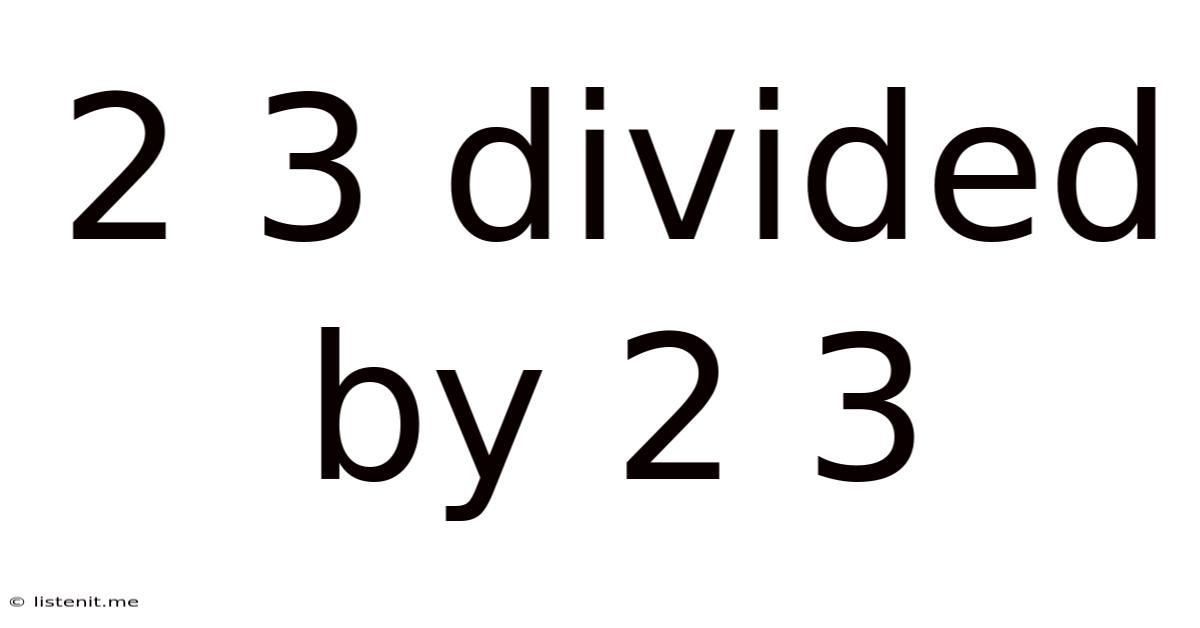
Table of Contents
Delving Deep into the Enigma: 2/3 Divided by 2/3
The seemingly simple mathematical expression, 2/3 divided by 2/3, often presents a stumbling block for many, particularly those who haven't fully grasped the nuances of fraction division. While the answer might seem obvious at first glance, a deeper exploration reveals a wealth of underlying concepts crucial for understanding more complex mathematical operations. This article will meticulously dissect this seemingly simple problem, clarifying the method, exploring the underlying principles, and extending the concept to more advanced applications.
Understanding Fraction Division: A Foundational Approach
Before diving into the specific problem of 2/3 divided by 2/3, let's solidify our understanding of fraction division. Remember the fundamental principle: dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal, or multiplicative inverse, of a fraction is obtained by simply swapping its numerator and denominator.
For instance, the reciprocal of 2/3 is 3/2. Therefore, any division problem involving fractions can be transformed into a multiplication problem, simplifying the process significantly. This crucial concept eliminates the confusion often associated with directly dividing fractions.
Solving 2/3 Divided by 2/3: A Step-by-Step Guide
Now, let's tackle the problem at hand: 2/3 ÷ 2/3. Applying the principle of reciprocals, we can rewrite the problem as:
2/3 x 3/2
Now, we simply multiply the numerators together and the denominators together:
(2 x 3) / (3 x 2) = 6/6
Finally, we simplify the resulting fraction:
6/6 = 1
Therefore, the solution to 2/3 divided by 2/3 is 1.
Beyond the Basic: Exploring the Conceptual Implications
While the mathematical process is straightforward, understanding the underlying concepts provides a deeper appreciation of the result. Dividing a number by itself always results in 1. This is a fundamental principle of mathematics, applicable to any number, including fractions. The problem 2/3 ÷ 2/3 is essentially asking: "How many times does 2/3 fit into 2/3?" The answer, intuitively and mathematically, is one time.
Practical Applications: Real-World Examples
The concept of dividing fractions, and the specific case of 2/3 divided by 2/3, finds applications in numerous real-world scenarios. Imagine you have 2/3 of a pizza, and you want to share it equally among groups, each receiving 2/3 of the pizza. How many groups can you serve? The answer, derived from 2/3 ÷ 2/3, is one group.
Consider another example: you have 2/3 of a cup of flour, and a recipe requires 2/3 of a cup. How many times can you use the flour according to the recipe's requirement? Again, the answer is one. These seemingly simple scenarios highlight the practical relevance of understanding fraction division.
Extending the Concept: More Complex Fraction Divisions
Understanding 2/3 ÷ 2/3 lays the foundation for tackling more complex fraction division problems. Let's consider a slightly more challenging example: 1/2 ÷ 2/5.
Following the same principles:
1/2 ÷ 2/5 = 1/2 x 5/2 = (1 x 5) / (2 x 2) = 5/4
This example demonstrates the versatility of the reciprocal method. It’s adaptable to various fraction combinations, allowing for efficient and accurate solutions.
Tackling Mixed Numbers: A Step-by-Step Approach
The principles discussed also apply when dealing with mixed numbers (a whole number and a fraction). To divide mixed numbers, we first convert them into improper fractions (where the numerator is greater than or equal to the denominator). For example, let's consider 1 1/2 ÷ 2/3.
-
Convert mixed number to improper fraction: 1 1/2 = (1 x 2 + 1) / 2 = 3/2
-
Apply the reciprocal method: 3/2 ÷ 2/3 = 3/2 x 3/2 = 9/4
-
Simplify (if possible): 9/4 can also be expressed as 2 1/4
This demonstrates how the same fundamental principles can be seamlessly integrated to solve problems involving mixed numbers.
Decimal Equivalents: An Alternative Perspective
While fraction division is often preferred for accuracy, converting fractions to their decimal equivalents can offer an alternative approach. In our original problem, 2/3 is approximately 0.667 (rounded). Dividing 0.667 by 0.667 will also yield approximately 1, illustrating the equivalence of the two methods. However, it's crucial to remember that decimal approximations might introduce minor inaccuracies, making fraction division the preferred method for precision, especially in scientific and engineering applications.
Error Analysis and Common Mistakes
Even though the concept is relatively straightforward, certain common errors can creep into the calculation. One common mistake is forgetting to take the reciprocal of the divisor (the number you are dividing by). Another common pitfall is incorrectly multiplying or simplifying the fractions. Careful attention to detail and a thorough understanding of the process can minimize these errors.
Advanced Applications: Algebra and Beyond
The basic principles of fraction division extend far beyond simple arithmetic. In algebra, you'll encounter variables and expressions involving fractions. The core concept of using the reciprocal remains the same. For instance, solving an equation like (x/3) ÷ (2x/9) = 1 requires applying the same principles. This highlights the fundamental nature of the concept and its pervasive application across various mathematical domains.
Conclusion: Mastering Fraction Division
The simple expression, 2/3 divided by 2/3, while seemingly trivial, offers a powerful entry point into the world of fraction division. By mastering this fundamental concept, we unlock a deeper understanding of mathematical operations, build a stronger foundation for tackling more complex problems, and gain valuable problem-solving skills applicable in numerous real-world contexts. The consistent application of the reciprocal method, along with a thorough understanding of fraction manipulation, ensures accuracy and confidence in solving any fraction division problem. Remember to always check your work and practice regularly to reinforce your understanding. The journey from simple fractions to advanced algebraic manipulations hinges on this seemingly simple yet crucial principle.
Latest Posts
Latest Posts
-
Spane Scale Of Emotion Research Project
Jun 05, 2025
-
Definition Of Channel Protein In Biology
Jun 05, 2025
-
Castor Oil And The Lymphatic System
Jun 05, 2025
-
How Much Fetal Fraction Is Needed For Gender
Jun 05, 2025
-
Florence Nightingale And Evidence Based Practice
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.