18 Of 25 Is What Percent
listenit
May 25, 2025 · 5 min read
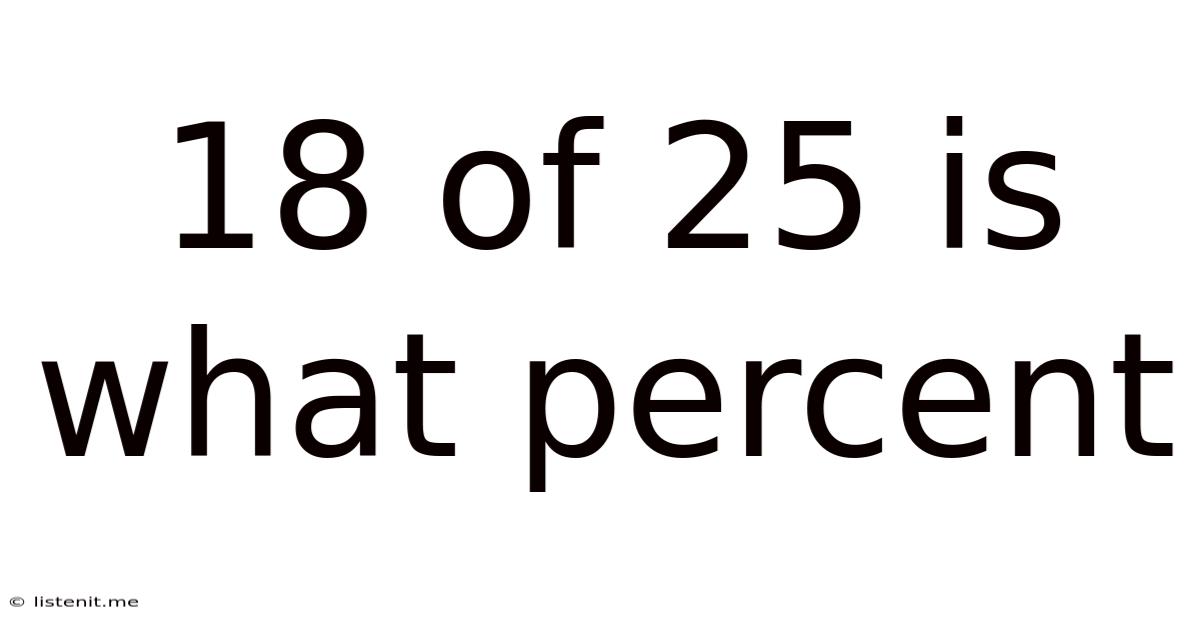
Table of Contents
18 out of 25 is What Percent? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to determine percentages allows for clear comparisons, effective data interpretation, and informed decision-making. This comprehensive guide will delve into the calculation of "18 out of 25 is what percent?", providing not only the answer but also a detailed explanation of the underlying methodology, practical applications, and related percentage problems.
Understanding Percentages
A percentage represents a fraction of 100. The term "percent" literally means "per hundred" (from the Latin per centum). Therefore, expressing a value as a percentage shows its proportional relationship to 100. For instance, 50% signifies 50 out of 100, or one-half.
Calculating "18 out of 25 is What Percent?"
To determine what percentage 18 represents out of 25, we'll employ a simple yet powerful method:
1. Formulate the Fraction:
First, express the given values as a fraction: 18/25. This fraction shows the part (18) relative to the whole (25).
2. Convert the Fraction to a Decimal:
To change a fraction to a decimal, divide the numerator (18) by the denominator (25):
18 ÷ 25 = 0.72
3. Convert the Decimal to a Percentage:
Multiply the decimal value by 100 and add the percent symbol (%):
0.72 × 100 = 72%
Therefore, 18 out of 25 is 72%.
Alternative Calculation Method: Using Proportions
Another approach involves setting up a proportion:
- Let 'x' represent the unknown percentage.
- We can set up the proportion: 18/25 = x/100
To solve for 'x', cross-multiply:
25x = 1800
Divide both sides by 25:
x = 1800 ÷ 25 = 72
Therefore, x = 72%, confirming our previous result.
Practical Applications of Percentage Calculations
Percentage calculations are invaluable in numerous real-world situations:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all involve percentages. Understanding percentage changes helps analyze financial growth or decline. For example, if you invested $1000 and earned $72 in interest, you earned 72% of your initial investment as interest.
-
Statistics: Percentages are crucial for representing data and interpreting results in statistical analysis. For instance, if a survey shows that 72% of respondents prefer a particular product, this provides a strong indication of consumer preference. Analyzing survey results and presenting them in percentage terms is an important skill.
-
Science: In scientific experiments and research, percentages are frequently used to express concentrations, yields, and error margins. For example, a 72% yield in a chemical reaction indicates that 72% of the expected product was obtained.
-
Education: Grading systems often use percentages to represent student performance. Scoring 18 out of 25 on a test translates to a 72% score, and is often vital in determining academic success.
-
Everyday Life: Calculating tips at restaurants, understanding sales discounts in shops, and determining the nutritional content of food all involve percentage calculations. For example, a 72% off sale means significant savings. Knowing the percentage of fat in food helps make informed dietary choices.
Related Percentage Problems and Calculations
Let's explore some related problems to further solidify understanding:
1. What is 72% of 25?
This problem is the reverse of our original calculation. To find 72% of 25, we convert the percentage to a decimal (72/100 = 0.72) and multiply it by 25:
0.72 × 25 = 18
This confirms that 72% of 25 is indeed 18.
2. 25 is what percent of 18?
This problem changes the context. We follow the same steps:
- Form the fraction: 25/18
- Convert to decimal: 25 ÷ 18 ≈ 1.3889
- Convert to percentage: 1.3889 × 100 ≈ 138.89%
In this case, 25 is approximately 138.89% of 18. This highlights that percentages can be greater than 100%, representing values exceeding the whole.
3. 18 is what percent of 50?
- Form the fraction: 18/50
- Convert to decimal: 18 ÷ 50 = 0.36
- Convert to percentage: 0.36 × 100 = 36%
Therefore, 18 is 36% of 50. This showcases how changes in the base number affect the resulting percentage.
4. Increasing and Decreasing Percentages:
Frequently, we need to calculate percentage increases or decreases. For example, if a price increases by 10%, we first find the 10% increase and then add it to the original price. Conversely, for a percentage decrease, we subtract the percentage decrease from the original value.
Example: If a product costs $50 and its price increases by 20%, the new price will be:
- 20% of $50 = (20/100) x $50 = $10
- New price = $50 + $10 = $60
If the same $50 product decreases by 20%, the new price will be:
- 20% of $50 = (20/100) x $50 = $10
- New price = $50 - $10 = $40
Mastering Percentage Calculations: Tips and Tricks
-
Memorize common percentage equivalents: Knowing that 1/4 = 25%, 1/2 = 50%, and 3/4 = 75% can speed up calculations significantly.
-
Use a calculator: For complex calculations, a calculator can efficiently handle the arithmetic operations.
-
Practice regularly: Consistent practice will build proficiency and confidence in performing percentage calculations.
-
Understand the context: The meaning of a percentage depends heavily on its context. Always consider the base value.
-
Check your work: Verify your calculations to ensure accuracy.
Conclusion
Calculating percentages is a versatile skill applicable in many facets of life. Understanding the fundamental methods, coupled with regular practice, will empower you to tackle various percentage problems efficiently and confidently. The seemingly simple question, "18 out of 25 is what percent?", serves as a gateway to a broader understanding of a critical mathematical concept. By mastering these techniques, you'll be well-equipped to analyze data, make informed decisions, and navigate the numerical world with ease. Remember to always consider the context of your percentage calculation to ensure you are correctly interpreting the results.
Latest Posts
Latest Posts
-
How Many Days Since Sep 15
May 26, 2025
-
How Many Days Away Is March 15
May 26, 2025
-
How To Figure Tile For Shower
May 26, 2025
-
4 Times As Much As 35
May 26, 2025
-
72 As A Fraction In Simplest Form
May 26, 2025
Related Post
Thank you for visiting our website which covers about 18 Of 25 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.