16 Out Of 25 Is Equal To What Percent
listenit
May 12, 2025 · 5 min read
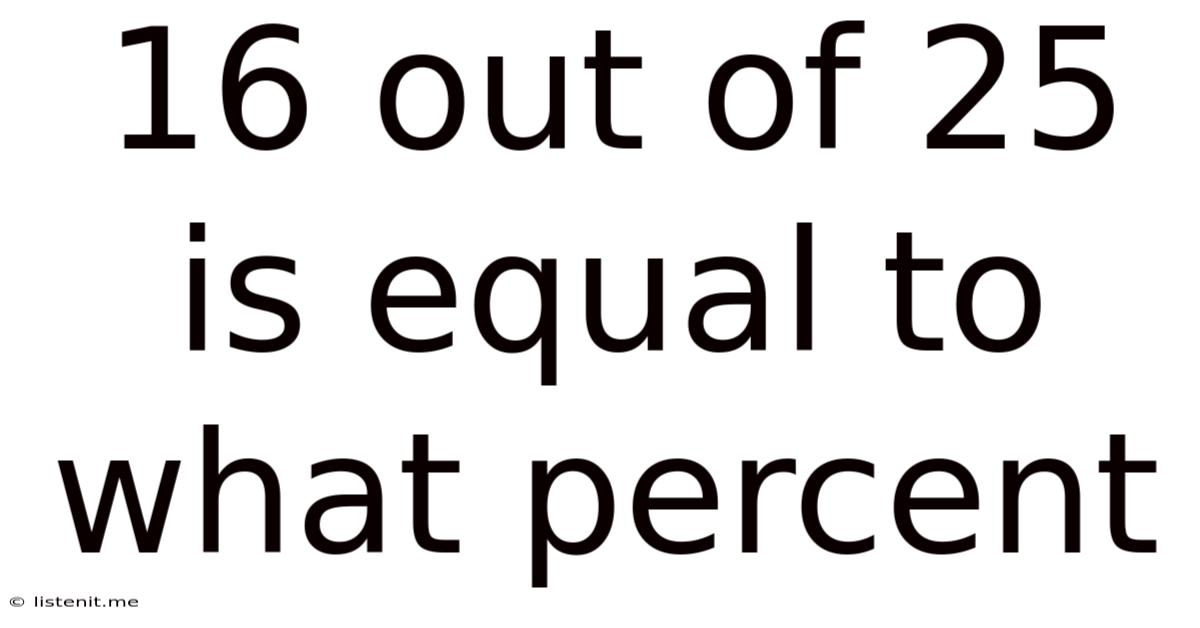
Table of Contents
16 out of 25 is Equal to What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and taxes to comprehending statistical data and analyzing financial reports. This comprehensive guide will delve into the question, "16 out of 25 is equal to what percent?", providing not only the answer but also a detailed explanation of the process, various calculation methods, and practical applications. We'll explore different approaches to solving percentage problems and equip you with the knowledge to confidently tackle similar calculations in the future.
Understanding Percentages: The Basics
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be represented as a fraction with a denominator of 100. For instance, 50% is equivalent to 50/100, which simplifies to 1/2.
Key Components:
- Part: This represents the specific portion of the whole we're interested in. In our case, the part is 16.
- Whole: This is the total amount or the complete entity. In our problem, the whole is 25.
- Percentage: This is the ratio of the part to the whole, expressed as a number out of 100. This is what we need to calculate.
Method 1: Using the Formula
The most straightforward method to calculate a percentage is using a simple formula:
(Part / Whole) * 100% = Percentage
Let's apply this to our problem:
(16 / 25) * 100% = Percentage
- Divide the part by the whole: 16 / 25 = 0.64
- Multiply the result by 100%: 0.64 * 100% = 64%
Therefore, 16 out of 25 is equal to 64%.
Method 2: Converting to a Fraction
Another effective approach involves first converting the given numbers into a fraction and then converting that fraction into a percentage.
- Express as a fraction: The problem "16 out of 25" can be written as the fraction 16/25.
- Convert to an equivalent fraction with a denominator of 100: To do this, we need to find a number that, when multiplied by 25, equals 100. That number is 4. We multiply both the numerator and the denominator by 4: (16 * 4) / (25 * 4) = 64/100.
- Express as a percentage: Since the denominator is now 100, the numerator represents the percentage directly. Thus, 64/100 is equal to 64%.
Method 3: Using Proportions
Proportions offer a versatile method for solving percentage problems. We set up a proportion where one ratio represents the known values (part and whole) and the other ratio represents the unknown percentage (x/100).
- Set up the proportion: 16/25 = x/100
- Cross-multiply: 16 * 100 = 25 * x
- Solve for x: 1600 = 25x => x = 1600 / 25 = 64
- Express as a percentage: x = 64%, confirming our previous results.
Practical Applications of Percentage Calculations
The ability to calculate percentages is incredibly valuable in various real-world scenarios. Here are just a few examples:
1. Retail and Sales:
- Discounts: Calculating discounts offered during sales events. For example, a 20% discount on a $100 item would be calculated as (20/100) * $100 = $20.
- Taxes: Determining the amount of sales tax or VAT added to purchases.
- Profit Margins: Calculating the profit percentage earned on sales.
2. Finance and Investments:
- Interest Rates: Calculating simple or compound interest on loans or investments.
- Return on Investment (ROI): Assessing the profitability of an investment.
- Financial Statements: Analyzing financial reports to understand percentages of revenue, expenses, and profits.
3. Statistics and Data Analysis:
- Data Representation: Presenting data visually using percentages in charts and graphs.
- Statistical Significance: Determining the significance of data using percentages.
- Surveys and Polls: Interpreting survey results presented as percentages.
4. Everyday Life:
- Tip Calculation: Calculating a gratuity at a restaurant.
- Recipe Scaling: Adjusting recipe ingredients based on the number of servings.
- Grade Calculation: Determining a grade percentage based on scores on tests and assignments.
Beyond the Basics: More Complex Percentage Problems
While the problem "16 out of 25" is relatively straightforward, percentage calculations can become more intricate. Consider these examples:
- Finding the whole when given the part and the percentage: If you know that 20% of a number is 10, you can use the formula: (Part / Percentage) * 100 = Whole. In this case, (10 / 20) * 100 = 50.
- Finding the part when given the whole and the percentage: If you need to find 30% of 200, you can calculate (30/100) * 200 = 60.
- Percentage change: This involves calculating the increase or decrease in a value over time, expressed as a percentage. The formula is: [(New Value - Old Value) / Old Value] * 100%.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The key to mastering percentages is consistent practice. Work through various problems, starting with simple ones and gradually increasing the complexity.
- Understand the Concepts: A solid grasp of the underlying concepts is crucial. Make sure you understand the relationship between fractions, decimals, and percentages.
- Use Different Methods: Experiment with different calculation methods to find the approach that best suits your understanding and problem-solving style.
- Check Your Answers: Always verify your answers to ensure accuracy. You can often check your work using alternative methods.
- Utilize Online Resources: Many online resources, including calculators and tutorials, can aid in understanding and solving percentage problems.
Conclusion
Calculating percentages is a vital skill with widespread applications. Understanding the fundamental concepts and applying the appropriate methods will allow you to confidently tackle percentage problems in various contexts, from everyday life to professional settings. Remember the core formula – (Part / Whole) * 100% – and practice regularly to solidify your understanding. By mastering percentages, you'll be better equipped to analyze data, make informed decisions, and navigate numerous aspects of life more effectively. The answer to "16 out of 25 is equal to what percent?" is definitively 64%, a fundamental understanding readily applicable to a vast array of practical scenarios.
Latest Posts
Related Post
Thank you for visiting our website which covers about 16 Out Of 25 Is Equal To What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.