150 Of What Number Is 48
listenit
May 12, 2025 · 4 min read
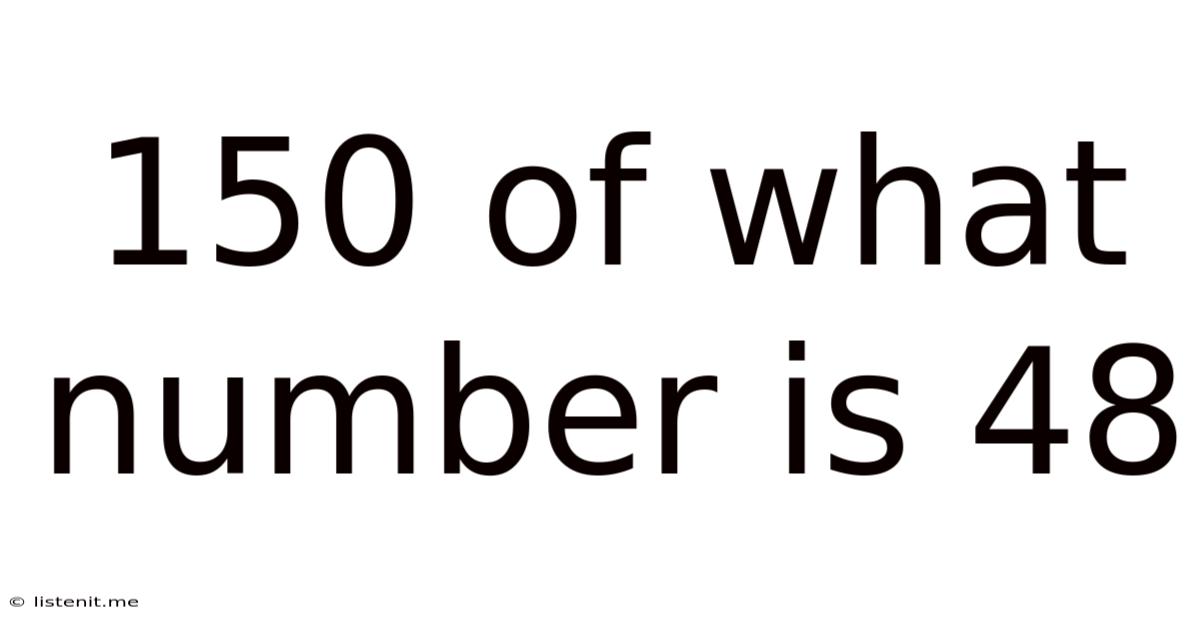
Table of Contents
150% of What Number is 48? A Comprehensive Guide to Percentage Calculations
Finding the original number when you know a percentage and its value is a common mathematical problem. This article delves deep into solving the question: "150% of what number is 48?" We'll explore various methods, from basic algebra to using proportions and even discussing practical applications of percentage calculations in real-world scenarios. Understanding these concepts is crucial for anyone working with percentages, whether it's in finance, statistics, or everyday life.
Understanding Percentages and Their Applications
Before diving into the solution, let's quickly refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Percentages are used extensively across numerous fields:
- Finance: Calculating interest rates, discounts, profit margins, taxes.
- Statistics: Representing data, analyzing trends, and drawing conclusions from samples.
- Science: Expressing concentrations, error margins, and experimental results.
- Everyday Life: Calculating tips, understanding sales, comparing prices.
Method 1: Using Algebra to Solve for the Unknown
This method involves setting up an algebraic equation and solving for the unknown variable. Let's represent the unknown number as 'x'. The problem states that 150% of x is 48. We can translate this into an equation:
1.5x = 48
To solve for x, we need to isolate it by dividing both sides of the equation by 1.5:
x = 48 / 1.5
x = 32
Therefore, 150% of 32 is 48.
Method 2: Using Proportions
Proportions offer another straightforward approach to solving percentage problems. A proportion is an equation that states two ratios are equal. We can set up a proportion to represent the problem:
150/100 = 48/x
This proportion reads: "150 is to 100 as 48 is to x". To solve for x, we cross-multiply:
150x = 4800
Now, divide both sides by 150:
x = 4800 / 150
x = 32
Again, we find that x = 32. This confirms our answer from the algebraic method.
Method 3: Understanding the Percentage Increase
The problem presents a scenario where the original number is increased by 50% (150% - 100% = 50%) to reach 48. We can approach this by considering the increase as a separate component:
Let's say the original number is 'x'. A 50% increase of 'x' is represented as 0.5x. Therefore, the new number (48) is the original number plus the 50% increase:
x + 0.5x = 48
Combining the terms with 'x':
1.5x = 48
This equation is identical to the one we derived using the algebraic method. Solving for x yields the same result: x = 32.
Practical Applications and Real-World Examples
Understanding percentage calculations is vital for numerous real-world applications. Here are a few examples:
-
Sales and Discounts: A store offers a 20% discount on an item priced at $60. To find the sale price, we calculate 20% of $60 and subtract it from the original price: 0.20 * $60 = $12; $60 - $12 = $48.
-
Interest Calculations: If you invest $32 and earn 50% interest, your earnings will be 0.50 * $32 = $16, resulting in a total of $48.
-
Tax Calculations: If a product costs $32 before tax, and the tax rate is 50%, the total cost will be $32 + ($32 * 0.50) = $48.
-
Data Analysis: Suppose a survey shows that 48 out of 150 people prefer a certain brand. To express this as a percentage, we calculate (48/150) * 100% = 32%. This indicates that 32% of the respondents prefer the brand.
Expanding Your Understanding: Working with Different Percentages
The methods discussed above can be easily adapted to solve problems with different percentages. For instance, if the question was "75% of what number is 48?", the equation would be:
0.75x = 48
Solving for x:
x = 48 / 0.75
x = 64
Similarly, you can apply these techniques to any percentage problem by converting the percentage to a decimal and solving the resulting equation.
Troubleshooting Common Mistakes
When working with percentages, common mistakes can lead to incorrect results. Here are some points to keep in mind:
-
Incorrect Decimal Conversion: Always convert percentages to decimals correctly before using them in calculations. For example, 150% is 1.5, not 0.15.
-
Order of Operations: Follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Rounding Errors: Be mindful of rounding errors, especially when working with multiple decimal places. Round your final answer to an appropriate number of decimal places depending on the context of the problem.
Conclusion: Mastering Percentage Calculations
Understanding how to solve problems like "150% of what number is 48?" is a fundamental skill with numerous practical applications. By mastering the various methods presented in this article – using algebra, proportions, or by considering the percentage increase – you can confidently tackle a wide range of percentage calculations. Remember to practice regularly and be aware of potential pitfalls to achieve accuracy and proficiency in this important mathematical skill. The ability to confidently manipulate percentages will significantly improve your problem-solving capabilities and your understanding of numerical data in various aspects of your life.
Latest Posts
Latest Posts
-
How Many Feet Is 2 7 Meters
May 13, 2025
-
Difference Between Natural Selection And Selective Breeding
May 13, 2025
-
What Is The Primary Function Of Cellular Respiration
May 13, 2025
-
Copper Has Two Isotopes Copper 63 And Copper 65
May 13, 2025
-
7 Is What Percent Of 49
May 13, 2025
Related Post
Thank you for visiting our website which covers about 150 Of What Number Is 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.