15 Out Of 24 As A Percentage
listenit
May 26, 2025 · 5 min read
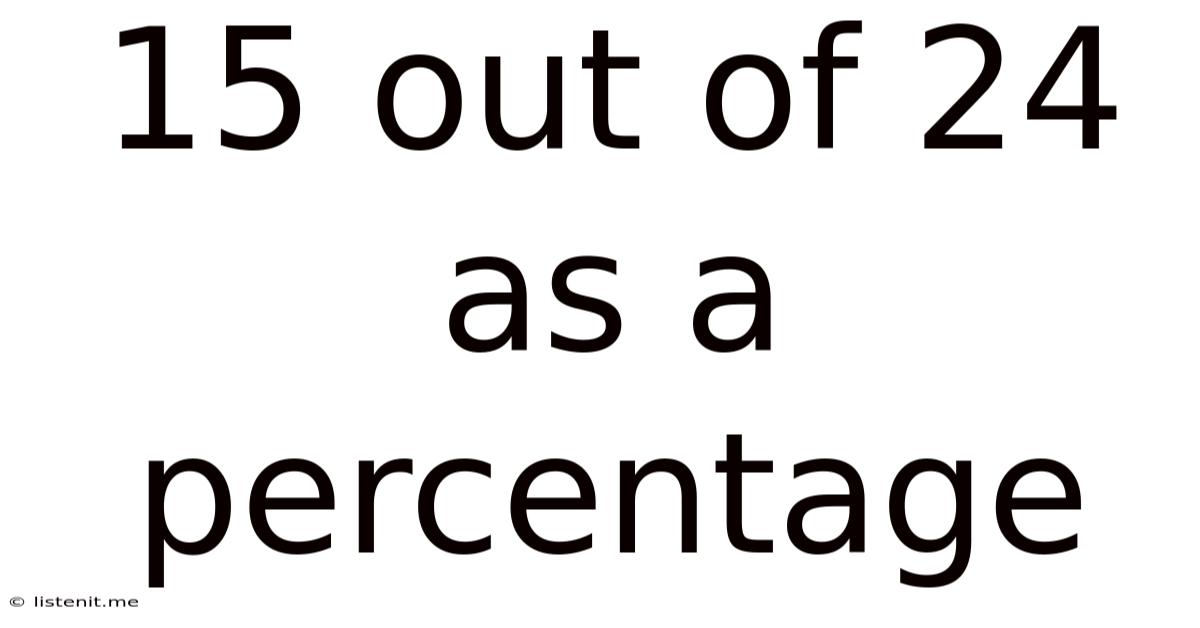
Table of Contents
15 out of 24 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from academic studies and financial analysis to everyday life scenarios. Understanding how to convert fractions and ratios into percentages is crucial for making informed decisions and interpreting data effectively. This article delves into the specifics of calculating "15 out of 24 as a percentage," offering a step-by-step guide, exploring different calculation methods, and providing practical examples to solidify your understanding.
Understanding Percentages
A percentage represents a fraction of 100. The term "percent" originates from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be expressed as a fraction with a denominator of 100. For instance, 25% is equivalent to 25/100, which simplifies to 1/4.
Calculating 15 out of 24 as a Percentage: The Basic Method
The most straightforward method for calculating 15 out of 24 as a percentage involves three simple steps:
-
Form a Fraction: Express the given numbers as a fraction. In this case, 15 out of 24 is represented as 15/24.
-
Convert to Decimal: Divide the numerator (15) by the denominator (24). This gives you a decimal value: 15 ÷ 24 = 0.625
-
Convert Decimal to Percentage: Multiply the decimal value by 100 to express it as a percentage. 0.625 × 100 = 62.5%
Therefore, 15 out of 24 is equal to 62.5%.
Alternative Calculation Methods
While the basic method is effective, exploring alternative approaches can enhance your understanding and provide flexibility depending on the context.
Method 2: Simplifying the Fraction
Before converting to a decimal, simplify the fraction 15/24 by finding the greatest common divisor (GCD) of 15 and 24. The GCD of 15 and 24 is 3. Dividing both the numerator and denominator by 3 simplifies the fraction to 5/8. Now, divide 5 by 8 (5 ÷ 8 = 0.625) and multiply by 100 to get 62.5%. This method streamlines the calculation and minimizes the risk of errors in decimal division.
Method 3: Using Proportions
You can set up a proportion to solve for the percentage:
15/24 = x/100
Cross-multiply: 24x = 1500
Solve for x: x = 1500/24 = 62.5
Therefore, x = 62.5%, confirming our previous calculations. This method is particularly helpful when dealing with more complex percentage problems.
Practical Applications and Real-World Examples
Understanding percentage calculations has numerous applications in various real-world scenarios. Here are a few examples where calculating "15 out of 24 as a percentage" might be relevant:
-
Academic Performance: If a student answered 15 out of 24 questions correctly on a test, their score would be 62.5%.
-
Sales and Marketing: If a salesperson made 15 sales out of 24 potential clients, their conversion rate would be 62.5%.
-
Manufacturing and Quality Control: If 15 out of 24 manufactured items passed quality checks, the pass rate is 62.5%.
-
Financial Analysis: If an investment yielded a profit of 15 units out of a total investment of 24 units, the return on investment (ROI) is 62.5%.
-
Sports Statistics: If a basketball player made 15 out of 24 shots, their shooting percentage is 62.5%.
These examples demonstrate how the seemingly simple calculation of 15 out of 24 as a percentage can have far-reaching implications across various disciplines.
Beyond the Basics: Advanced Percentage Concepts
While calculating 15 out of 24 as a percentage provides a foundation in percentage calculations, it's crucial to grasp more advanced concepts for a comprehensive understanding.
Percentage Increase and Decrease
Determining percentage increase or decrease requires understanding the initial and final values. The formula for percentage change is:
[(Final Value - Initial Value) / Initial Value] × 100
For instance, if a value increases from 20 to 25, the percentage increase is [(25 - 20) / 20] × 100 = 25%. Conversely, if a value decreases from 25 to 20, the percentage decrease is [(20 - 25) / 25] × 100 = -20%.
Percentage Points vs. Percentage Change
It's important to differentiate between "percentage points" and "percentage change." A percentage point represents an absolute difference between two percentages, while percentage change indicates the relative change. For example, if interest rates increase from 5% to 8%, the increase is 3 percentage points, but the percentage change is [(8 - 5) / 5] × 100 = 60%.
Compound Interest
Compound interest involves earning interest on both the principal amount and accumulated interest. This results in exponential growth over time. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding compound interest is essential for financial planning and investment decisions.
Troubleshooting Common Errors in Percentage Calculations
Common errors in percentage calculations often stem from:
-
Incorrect Fraction Formation: Ensuring the correct numerator and denominator are used in the initial fraction is crucial.
-
Decimal Errors: Care must be taken during decimal division and multiplication to avoid rounding errors.
-
Unit Confusion: Remembering to multiply the decimal by 100 to express the result as a percentage is vital.
-
Misinterpreting Percentage Points: Confusing percentage points with percentage change can lead to inaccurate conclusions.
Conclusion: Mastering Percentage Calculations
Calculating 15 out of 24 as a percentage, while seemingly simple, serves as a gateway to understanding a broader range of percentage-related calculations. Mastering these concepts empowers you to confidently interpret data, make informed decisions, and excel in various academic and professional settings. By understanding the fundamental methods, exploring alternative approaches, and being aware of potential pitfalls, you can build a robust understanding of percentage calculations and apply them effectively in numerous real-world scenarios. Remember to practice regularly and apply these techniques to different problems to solidify your grasp of this essential mathematical skill.
Latest Posts
Latest Posts
-
Colloids And Surfaces A Physicochemical And Engineering Aspects Impact Factor
May 27, 2025
-
Food Research International Journal Impact Factor
May 27, 2025
-
Impact Factor Journal Of Surgical Education
May 27, 2025
-
Surfaces And Interfaces Impact Factor 2023
May 27, 2025
-
Gait And Posture Journal Impact Factor
May 27, 2025
Related Post
Thank you for visiting our website which covers about 15 Out Of 24 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.