15 Of What Number Is 12
listenit
May 10, 2025 · 4 min read
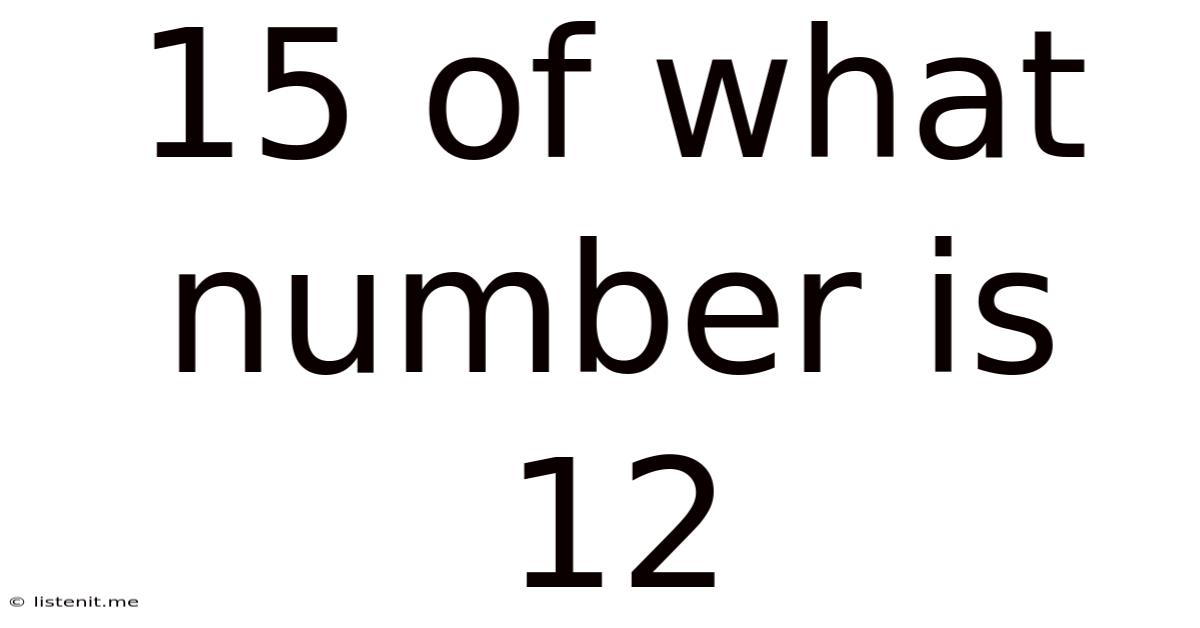
Table of Contents
15% of What Number is 12? A Deep Dive into Percentage Calculations
Finding the whole from a percentage and a part is a fundamental concept in mathematics, with widespread applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will comprehensively explore how to solve the problem "15% of what number is 12," explaining the different methods, illustrating each step clearly, and expanding on the broader concepts involved. We'll also delve into real-world applications to solidify your understanding.
Understanding Percentages and Their Components
Before tackling the problem directly, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The formula to calculate a percentage is:
(Percentage/100) * Whole = Part
In our problem, "15% of what number is 12," we know the percentage (15%) and the part (12). Our goal is to find the "whole" number. This requires rearranging the formula.
Method 1: Algebraic Approach
This method utilizes basic algebra to solve for the unknown "whole" number. We'll represent the whole number with the variable 'x'. The equation becomes:
(15/100) * x = 12
Now, we solve for 'x':
-
Simplify the fraction: 15/100 simplifies to 3/20. The equation now becomes:
(3/20) * x = 12
-
Multiply both sides by 20: This eliminates the fraction, leaving:
3x = 240
-
Divide both sides by 3: This isolates 'x', giving us the solution:
x = 80
Therefore, 15% of 80 is 12.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion as follows:
15/100 = 12/x
This proportion states that the ratio of 15 to 100 (15%) is equal to the ratio of 12 to the unknown whole number (x).
To solve for x:
-
Cross-multiply: Multiply 15 by x and 100 by 12:
15x = 1200
-
Divide both sides by 15: This isolates x:
x = 80
Again, we find that 15% of 80 is 12. This method reinforces the solution obtained through the algebraic approach.
Method 3: Using the Percentage Formula Rearranged
We can directly rearrange the percentage formula to solve for the whole:
Whole = (Part * 100) / Percentage
Substituting the known values:
Whole = (12 * 100) / 15
Whole = 1200 / 15
Whole = 80
This method provides a quick and efficient way to calculate the whole number, especially when dealing with simple percentages.
Real-World Applications: Where This Calculation Matters
Understanding how to calculate the whole from a percentage and a part has numerous practical applications:
1. Retail and Sales:
- Discount Calculations: Imagine a store offers a 15% discount on an item, and the discount amount is $12. Using the methods above, you can quickly calculate the original price of the item before the discount ($80).
- Sales Tax: If a sales tax of 15% adds $12 to the price of a product, you can determine the pre-tax price.
2. Finance and Investments:
- Investment Returns: If an investment yielded a 15% return of $12, you can calculate the initial investment amount.
- Interest Calculations: Simple interest calculations often involve finding the principal amount based on interest earned.
3. Data Analysis and Statistics:
- Sample Size Determination: In statistics, understanding percentages is crucial for calculating sample sizes and extrapolating results from a sample population to a larger population.
- Data Interpretation: Many statistical reports present data as percentages. Being able to work backward from a percentage and a part is vital for accurate data interpretation.
4. Everyday Life:
- Tip Calculations: Determining the pre-tip bill amount based on a 15% tip of $12.
- Recipe Scaling: Adjusting recipe ingredients when you only have a certain percentage of the original amount.
Expanding on Percentage Concepts: Beyond the Basics
This problem provides a foundation for understanding more complex percentage calculations. Here are some related concepts to explore:
- Compound Interest: Interest calculated not only on the principal but also on accumulated interest.
- Percentage Increase/Decrease: Calculating the percentage change between two values.
- Percentage Points: The difference between two percentages.
- Working with Multiple Percentages: Solving problems involving successive percentages (e.g., applying a discount and then a sales tax).
Mastering Percentage Calculations: Practice Makes Perfect
The key to mastering percentage calculations is consistent practice. Try solving similar problems with different percentages and parts. You can even create your own word problems to reinforce your understanding. Online resources and math textbooks provide numerous practice problems.
Conclusion: The Power of Percentage Understanding
The seemingly simple problem of "15% of what number is 12?" opens the door to a world of mathematical applications. By mastering the various methods for solving this type of problem – algebraic approach, proportions, and direct formula rearrangement – you equip yourself with a valuable skill applicable across diverse fields. Consistent practice and exploration of related percentage concepts will further solidify your understanding and empower you to tackle more complex percentage-related challenges confidently. Remember, the ability to manipulate percentages is a crucial skill in various aspects of life, and a strong grasp of these concepts will undoubtedly benefit you in both personal and professional endeavors.
Latest Posts
Latest Posts
-
Do Diastereomers Have The Same Chemical Properties
May 10, 2025
-
Solve The Equation On The Interval
May 10, 2025
-
Identify The Molecular Shape Of Each Lewis Structure
May 10, 2025
-
Parallelogram How Many Lines Of Symmetry
May 10, 2025
-
A Number X Is Greater Than 3
May 10, 2025
Related Post
Thank you for visiting our website which covers about 15 Of What Number Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.