14 Out Of 25 As A Percentage
listenit
May 24, 2025 · 4 min read
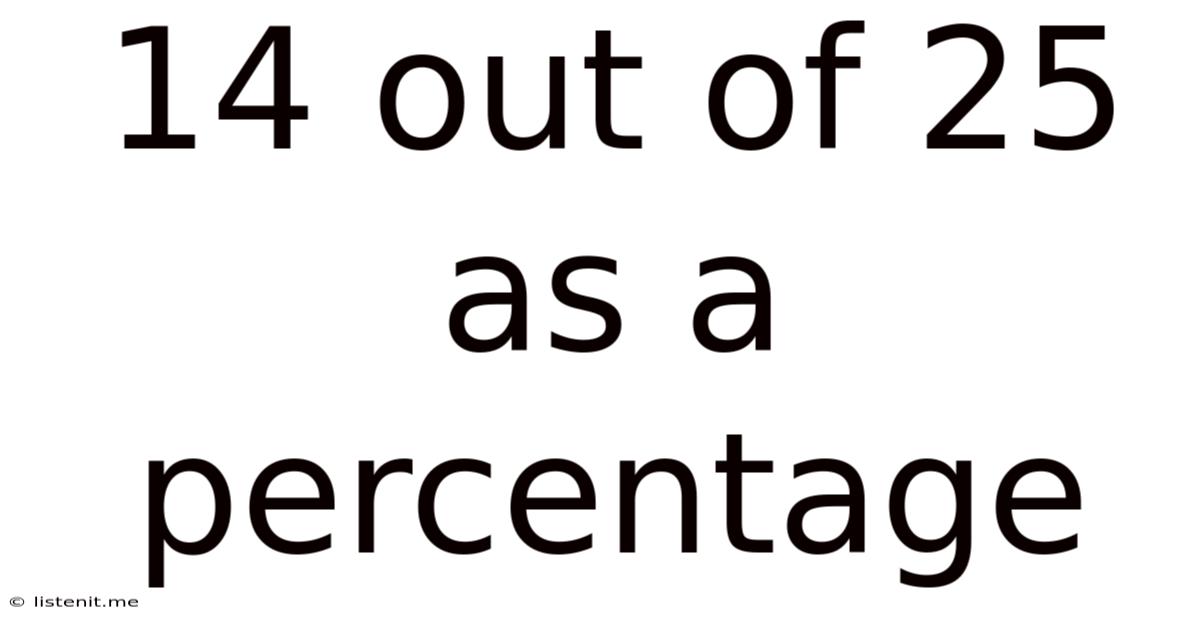
Table of Contents
14 out of 25 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with applications spanning various fields, from everyday budgeting to complex statistical analysis. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and communicating results effectively. This comprehensive guide will delve into the calculation of 14 out of 25 as a percentage, exploring different methods, practical applications, and common pitfalls to avoid. We will also touch upon broader percentage calculation techniques, empowering you to tackle similar problems with confidence.
Understanding Percentages: A Foundation
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction where the denominator is 100. It represents a proportion or rate out of a whole. The symbol "%" denotes a percentage. For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or 0.5 as a decimal.
Method 1: The Direct Conversion Method
This is the most straightforward approach to calculating 14 out of 25 as a percentage. We follow these steps:
-
Express as a fraction: Write the given numbers as a fraction: 14/25.
-
Convert to a decimal: Divide the numerator (14) by the denominator (25): 14 ÷ 25 = 0.56
-
Convert to a percentage: Multiply the decimal by 100%: 0.56 x 100% = 56%
Therefore, 14 out of 25 is 56%.
Method 2: Proportion Method
This method uses the concept of proportions to solve for the percentage. We set up a proportion equation:
14/25 = x/100
Here, 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
25x = 1400
Then, divide both sides by 25:
x = 1400 ÷ 25 = 56
Therefore, x = 56%, confirming our previous result. This method is particularly useful when dealing with more complex percentage problems where setting up a proportion provides a clearer path to the solution.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the calculation. Simply enter 14 ÷ 25 and then multiply the result by 100. The calculator will directly provide the answer: 56%. This method is efficient and minimizes the risk of manual calculation errors.
Practical Applications: Real-World Scenarios
Understanding percentage calculations is vital in numerous real-world situations. Here are some examples where calculating 14 out of 25 (or similar proportions) might be applied:
-
Academic Performance: If a student answers 14 out of 25 questions correctly on a test, their score is 56%.
-
Sales and Discounts: A store offering a 56% discount on an item is essentially giving you a reduction equivalent to 14 out of every 25 units of the original price.
-
Survey Results: If 14 out of 25 respondents in a survey answered "yes" to a particular question, 56% of respondents gave a positive response.
-
Financial Analysis: In investment analysis, percentages are fundamental for calculating returns on investment, analyzing growth rates, and understanding financial ratios. Understanding the proportion of successful investments versus unsuccessful ones is critical for assessing portfolio performance.
-
Sports Statistics: Calculating batting averages, free-throw percentages, and other sports statistics frequently involves similar percentage calculations.
Beyond 14 out of 25: Generalizing Percentage Calculations
The methods described above can be easily extended to calculate any fraction as a percentage. The general formula is:
(Numerator / Denominator) * 100% = Percentage
For example, to find what percentage 17 is of 20:
(17/20) * 100% = 85%
Common Mistakes to Avoid
Several common errors can lead to incorrect percentage calculations. These include:
-
Incorrect order of operations: Always perform division before multiplication when converting fractions to percentages.
-
Forgetting to multiply by 100: Remember that the result of the fraction must be multiplied by 100% to express it as a percentage.
-
Rounding errors: When dealing with decimals, pay attention to significant figures and avoid premature rounding. Round your final answer appropriately based on the context of the problem.
-
Confusing percentage change with percentage of a whole: These are distinct concepts. Percentage change represents the relative difference between two values, while percentage of a whole represents a part as a proportion of the whole.
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond calculating simple percentages, understanding percentage increases and decreases is essential. For example, if a price increases from $20 to $25, the percentage increase is calculated as:
[(New Value - Old Value) / Old Value] * 100% = [(25 - 20) / 20] * 100% = 25%
Similarly, a percentage decrease is calculated as:
[(Old Value - New Value) / Old Value] * 100%
These calculations are vital for tracking changes over time, analyzing growth rates, and understanding economic trends. They are applicable in various domains, including finance, economics, and data analysis.
Conclusion: Mastering Percentage Calculations
The ability to convert fractions into percentages is a crucial skill for navigating everyday life and tackling more complex problems. This guide has demonstrated multiple methods for calculating 14 out of 25 as a percentage – 56% – and highlighted the broad applicability of percentage calculations across diverse fields. By understanding the fundamentals and avoiding common mistakes, you'll enhance your problem-solving capabilities and improve your ability to interpret and communicate data effectively. Remember to practice these methods regularly to build your confidence and proficiency in handling percentage calculations. The more you practice, the more intuitive these calculations will become. Consistent practice is key to mastering this vital mathematical skill.
Latest Posts
Latest Posts
-
How Many Days Away Is May 24
May 24, 2025
-
How Many Years Ago Was 1968
May 24, 2025
-
What Is 15 Of An Hour
May 24, 2025
-
Round 99089 186735 To The Nearest Ten
May 24, 2025
-
What Is The Gcf Of 18 And 54
May 24, 2025
Related Post
Thank you for visiting our website which covers about 14 Out Of 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.