13 Out Of 16 As A Percent
listenit
May 09, 2025 · 4 min read
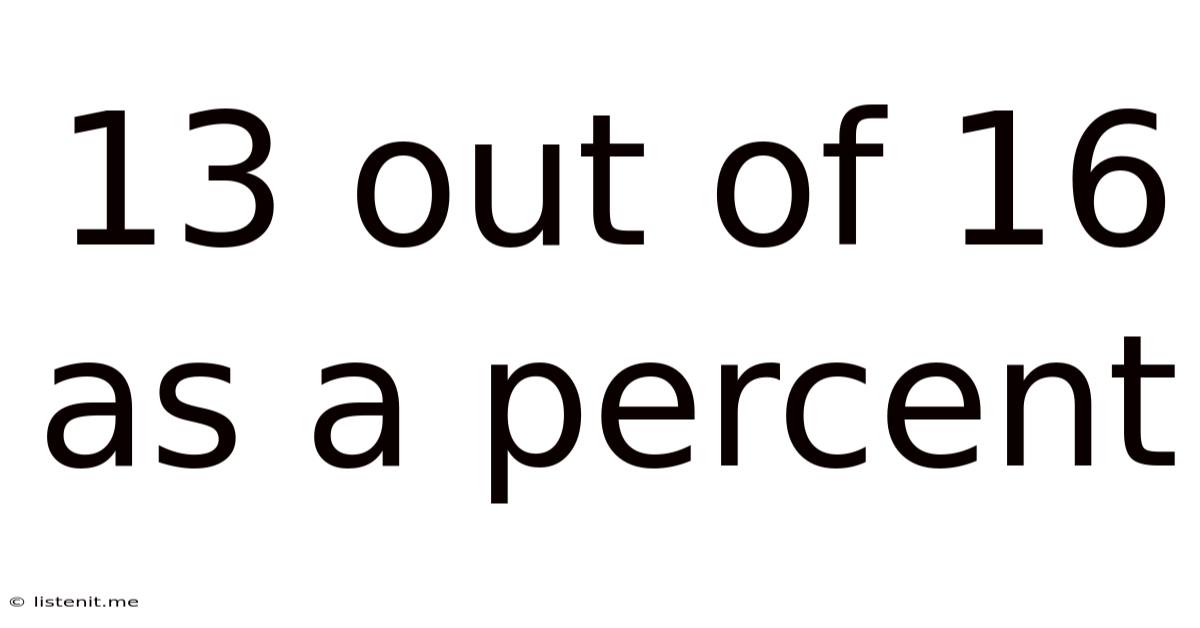
Table of Contents
13 out of 16 as a Percent: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various fields, from everyday finances to complex scientific analyses. Understanding how to convert fractions into percentages is crucial for making informed decisions and accurately interpreting data. This comprehensive guide will delve into the calculation of "13 out of 16 as a percent," exploring various methods and illustrating their practical applications. We'll also cover related concepts and address common misconceptions to solidify your understanding of percentage calculations.
Understanding Percentages
Before we dive into the specific calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "per hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 13 out of 16 as a Percentage: Method 1 - The Fraction Method
The most straightforward method to calculate 13 out of 16 as a percentage involves converting the fraction 13/16 into a percentage. Here's a step-by-step guide:
-
Express the ratio as a fraction: The statement "13 out of 16" can be directly expressed as the fraction 13/16.
-
Convert the fraction to a decimal: Divide the numerator (13) by the denominator (16): 13 ÷ 16 = 0.8125
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.8125 x 100 = 81.25
-
Add the percentage symbol: Therefore, 13 out of 16 is 81.25%.
Calculating 13 out of 16 as a Percentage: Method 2 - The Proportion Method
This method uses the concept of proportions to solve for the percentage. We set up a proportion where 'x' represents the percentage we want to find:
13/16 = x/100
To solve for 'x', we cross-multiply:
16x = 1300
Divide both sides by 16:
x = 1300 ÷ 16 = 81.25
Therefore, 13 out of 16 is 81.25%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios:
-
Academic Performance: Calculating grades, especially when weighted averages are involved, requires understanding percentages. For example, if a student scores 13 out of 16 on a quiz, their score is 81.25%.
-
Financial Matters: Percentages are crucial in finance. Calculating interest rates, discounts, taxes, and investment returns all involve percentage calculations. Understanding these calculations helps in making informed financial decisions.
-
Data Analysis: Percentages are commonly used to represent data in various forms like charts, graphs, and reports. This allows for a clear and concise representation of data, making it easier to understand trends and patterns. For example, if a survey shows that 13 out of 16 respondents prefer a particular product, the percentage (81.25%) provides a more impactful representation.
-
Scientific Research: In scientific fields like biology and chemistry, percentages are used to express concentrations, yields, and error margins. Accurate percentage calculations are essential for the reliability of research findings.
-
Everyday Life: From calculating tips at restaurants to understanding sales discounts in stores, percentages are embedded in our daily lives. Being proficient in percentage calculations simplifies these everyday tasks.
Common Mistakes to Avoid When Calculating Percentages
While percentage calculations are relatively straightforward, several common mistakes can lead to inaccurate results:
-
Incorrect order of operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when dealing with more complex calculations involving percentages.
-
Misunderstanding the context: Always carefully interpret the wording of the problem to ensure you are applying the correct calculation. For example, "13 out of 16" is different from "16 out of 13."
-
Rounding errors: Be mindful of rounding errors, especially when dealing with multiple percentage calculations. Rounding too early in the process can accumulate errors and lead to inaccurate final results.
-
Using the wrong formula: There are different formulas for calculating percentage increase, percentage decrease, and percentage change. Ensure you are using the appropriate formula for the problem at hand.
Expanding Your Understanding: Beyond the Basics
While this guide focuses on calculating "13 out of 16 as a percent," the principles discussed are applicable to a broader range of percentage calculations. Here are some related concepts to explore further:
-
Percentage Increase/Decrease: Learn how to calculate the percentage increase or decrease between two numbers. This is useful in tracking changes over time, such as population growth or price fluctuations.
-
Percentage Change: Understanding percentage change allows you to analyze the relative difference between two values. This is valuable in assessing the magnitude of changes in various contexts.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It's crucial for understanding financial growth over time.
-
Weighted Averages: When dealing with different weights or importance assigned to various values, weighted averages are employed. Mastering this concept is vital for calculating GPA, for example.
Conclusion: Mastering Percentage Calculations
The ability to accurately calculate percentages is a valuable asset in various aspects of life, both personal and professional. By understanding the fundamental concepts, employing the right methods, and avoiding common mistakes, you can confidently tackle percentage calculations. The example of "13 out of 16 as a percent," while seemingly simple, serves as a solid foundation for mastering more complex percentage problems. Remember to practice regularly to strengthen your skills and improve your understanding of this essential mathematical concept. With consistent effort and attention to detail, you can become proficient in calculating and interpreting percentages in any context.
Latest Posts
Latest Posts
-
Which Is Equivalent To 256 3 4
May 09, 2025
-
Square Root Of 162 Simplified Radical Form
May 09, 2025
-
Is Helium An Element Compound Or Mixture
May 09, 2025
-
Koh Strong Or Weak Acid Or Base
May 09, 2025
-
How Many Feet Is 100 Yard
May 09, 2025
Related Post
Thank you for visiting our website which covers about 13 Out Of 16 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.