13/52 X 13/52 X 13/52 X 13/52
listenit
May 12, 2025 · 6 min read
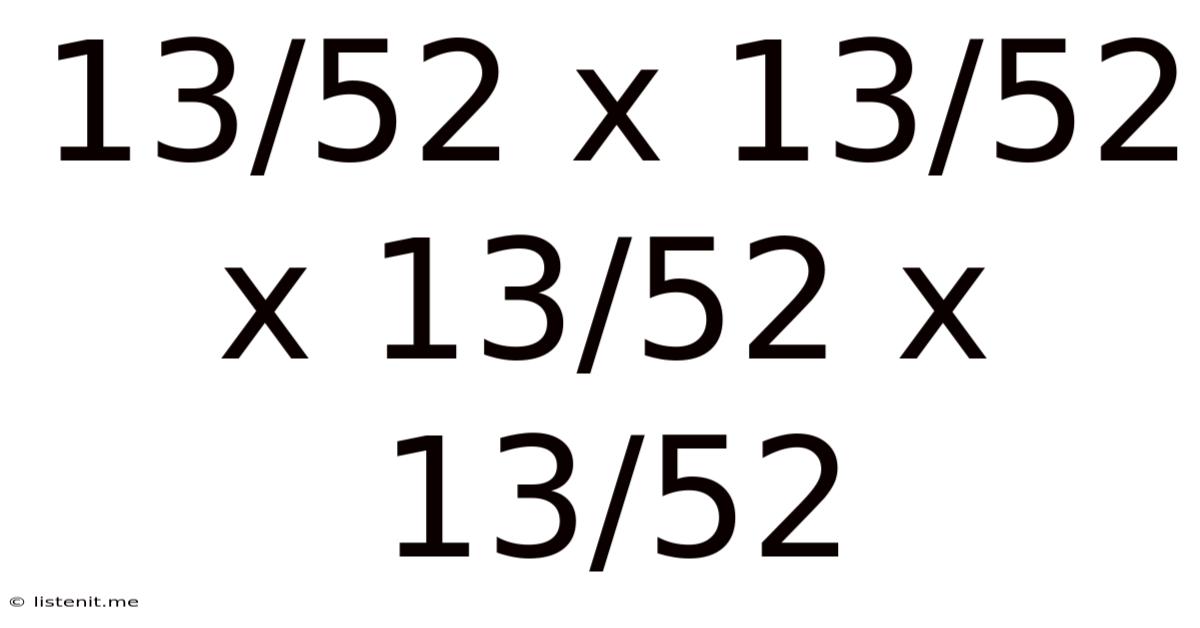
Table of Contents
Decoding the Probabilistic Puzzle: 13/52 x 13/52 x 13/52 x 13/52
The seemingly simple expression, 13/52 x 13/52 x 13/52 x 13/52, hides a fascinating world of probability, statistics, and the fundamental principles of chance. This seemingly innocuous calculation, frequently encountered in introductory probability courses and real-world scenarios, unravels the core concepts of independent events and their combined likelihood. Let's delve deep into this mathematical puzzle, exploring its implications and applications.
Understanding the Basics: Probability and Independent Events
Before we dissect the expression itself, let's solidify our understanding of the foundational concepts. Probability measures the likelihood of an event occurring. It's expressed as a number between 0 and 1, where 0 represents impossibility and 1 represents certainty. The expression 13/52, in the context of a standard deck of 52 playing cards, represents the probability of drawing a card of a specific suit (e.g., hearts) in a single draw. There are 13 cards of each suit in a standard deck.
Independent events are events where the outcome of one event does not influence the outcome of another. In our example, drawing a card, replacing it, and then drawing another card are independent events. The probability of drawing a heart on the second draw remains 13/52, regardless of the outcome of the first draw. This is crucial for understanding the multiplication involved in our expression.
Breaking Down the Expression: 13/52 x 13/52 x 13/52 x 13/52
Now, let's tackle the core of our investigation: 13/52 x 13/52 x 13/52 x 13/52. This expression represents the probability of a sequence of independent events occurring. Specifically, it calculates the probability of drawing a card of a specific suit four times in a row, replacing the card after each draw.
Each term, 13/52, represents the probability of drawing one card of a specific suit (e.g., hearts) from a standard deck of 52 cards. Since we replace the card after each draw, the probability remains constant for each draw. The multiplication signifies the calculation of the combined probability of all four events occurring sequentially.
To calculate the final probability, we simply multiply the individual probabilities:
13/52 x 13/52 x 13/52 x 13/52 = (13/52)^4 = (1/4)^4 = 1/256
Therefore, the probability of drawing a card of a specific suit four times in a row, with replacement, is 1/256, or approximately 0.0039. This means there's a roughly 0.39% chance of this event occurring.
Expanding the Scope: Applications and Interpretations
The seemingly simple calculation has broader implications across various fields. Let's explore some of these applications:
-
Games of Chance: Casinos rely heavily on probability calculations. Understanding the probability of specific outcomes in games like poker or blackjack is crucial for both players and casino operators. Our example directly relates to the probability of specific card sequences.
-
Quality Control: In manufacturing, the probability of multiple consecutive defects can be modeled using similar calculations. If there's a 1/100 chance of a defect in a single unit, the probability of finding four consecutive defective units (assuming independence) would follow the same logic.
-
Medical Diagnosis: In medical testing, the probability of multiple positive or negative results, assuming the tests are independent, can be calculated using this approach.
-
Genetics: The inheritance of genes can also be modeled using probability, particularly when considering independent events such as the inheritance of traits from separate chromosomes.
Beyond the Basics: Exploring Dependent Events
While our example focused on independent events, it's crucial to understand that many real-world scenarios involve dependent events, where the outcome of one event directly affects the probability of subsequent events.
Let's consider the scenario of drawing four cards of the same suit without replacement. In this case, the probabilities change with each draw. The probability of drawing a heart on the first draw is 13/52. However, if a heart is drawn, the probability of drawing another heart on the second draw becomes 12/51 (because there are only 12 hearts left and 51 cards total). The probability continues to decrease with each subsequent draw. Calculating this requires a different approach, involving conditional probability and combinations.
Delving Deeper: Combinations and Permutations
The expression 13/52 x 13/52 x 13/52 x 13/52 only considers the probability of drawing a specific suit four times in a row. It doesn't account for the order of the suits. If we wanted to calculate the probability of drawing four cards of any suit, the calculation becomes more complex. We would need to use combinations to account for the different possible sequences of suits.
For example, if we want to calculate the probability of drawing four cards of the same suit (regardless of which suit), we need to consider the four possible suits (hearts, diamonds, clubs, spades) and the probability of drawing each specific suit four times in a row.
This leads us to concepts like permutations and combinations, essential tools in probability and statistics. Permutations consider the order of events, while combinations only consider the selection of items without regard to order. Understanding these concepts is crucial for solving more complex probabilistic problems.
Practical Applications and Real-World Scenarios
Let’s consider some scenarios that mirror the mathematical concept we’ve explored:
-
Lottery Probabilities: While lottery draws are not strictly independent (due to ball removal), the calculations are similar. The probability of winning a lottery is exceedingly low due to the numerous possible combinations. Calculating this probability involves understanding combinations and the size of the sample space.
-
Predictive Modeling: Probability and statistics are pivotal in predictive modeling in various domains, from financial markets to weather forecasting. By analyzing past data, we can build models that predict future outcomes. The concepts of independent and dependent events are fundamental to these models.
-
Data Analysis: In data analysis, understanding probabilities is essential for interpreting results and making informed decisions. The reliability of statistical inferences hinges on sound probabilistic understanding.
Advanced Concepts and Further Exploration
To deepen your understanding, explore these advanced concepts:
-
Bayes' Theorem: This theorem is crucial for updating probabilities based on new evidence. It’s widely used in machine learning, medical diagnosis, and various other fields.
-
Conditional Probability: This concept deals with probabilities that depend on the occurrence of other events.
-
Stochastic Processes: These are mathematical models for systems that evolve randomly over time. They're used in various areas, from financial modeling to epidemiology.
Conclusion: The Power of Probability
The seemingly simple expression, 13/52 x 13/52 x 13/52 x 13/52, opens the door to a vast and fascinating world of probability and statistics. Understanding this expression, along with its underlying concepts, provides a foundation for comprehending chance, risk, and the likelihood of events in various aspects of life. From everyday decisions to complex scientific models, probability plays a crucial role in shaping our understanding of the world around us. The more you delve into this field, the more you appreciate its power and importance. By continuously exploring and expanding your knowledge of probability and statistics, you'll gain valuable tools for navigating the uncertainties of life and making more informed decisions.
Latest Posts
Latest Posts
-
Relationship Between Angular Momentum And Torque
May 12, 2025
-
What Happens To An Ecosystem When The Primary Consumers Disappear
May 12, 2025
-
What Structures Do Plant And Animal Cells Have In Common
May 12, 2025
-
How Many Protons And Neutrons Are In Nitrogen
May 12, 2025
-
Y 2x 5 Solve For Y
May 12, 2025
Related Post
Thank you for visiting our website which covers about 13/52 X 13/52 X 13/52 X 13/52 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.