13 1 2 As A Decimal
listenit
May 25, 2025 · 6 min read
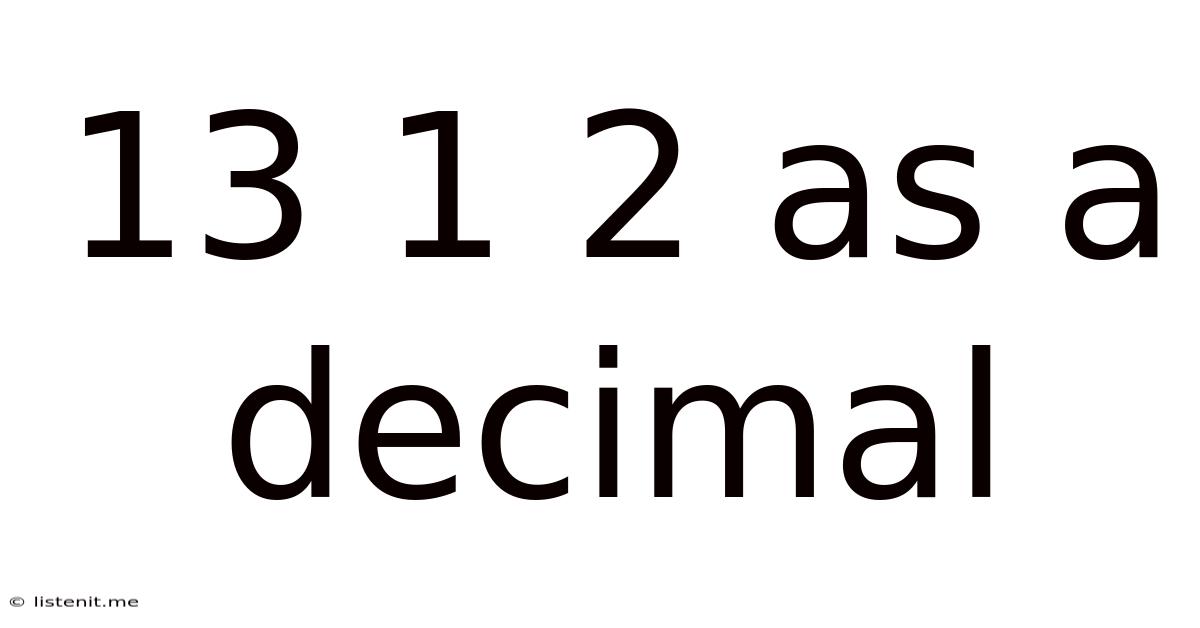
Table of Contents
13 1/2 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This article will delve deep into the conversion of the mixed number 13 1/2 into its decimal equivalent, explaining the process step-by-step and exploring the broader context of fraction-to-decimal conversions. We'll also discuss the practical applications of this conversion and address some frequently asked questions.
Understanding Mixed Numbers and Decimals
Before we jump into the conversion of 13 1/2, let's briefly recap the concepts of mixed numbers and decimals.
Mixed Numbers: A mixed number combines a whole number and a fraction, like 13 1/2. This represents 13 whole units and an additional half unit.
Decimals: Decimals represent numbers as a sum of powers of ten. The digits to the right of the decimal point represent fractions with denominators of 10, 100, 1000, and so on. For instance, 0.5 is equivalent to 5/10 or 1/2.
Converting 13 1/2 to a Decimal: The Methods
There are several ways to convert the mixed number 13 1/2 to its decimal equivalent. Let's explore the most common approaches:
Method 1: Converting the Fraction to a Decimal, then Adding the Whole Number
This is arguably the most straightforward method. We first convert the fraction 1/2 into a decimal and then add the whole number part.
-
Convert the fraction: The fraction 1/2 is equivalent to 0.5 (since 1 divided by 2 equals 0.5).
-
Add the whole number: Now, add the whole number part (13) to the decimal equivalent of the fraction (0.5): 13 + 0.5 = 13.5
Therefore, 13 1/2 as a decimal is 13.5.
Method 2: Converting the Entire Mixed Number to an Improper Fraction, then to a Decimal
This method involves first converting the mixed number into an improper fraction and then dividing the numerator by the denominator.
-
Convert to an improper fraction: To convert 13 1/2 to an improper fraction, we multiply the whole number (13) by the denominator (2), add the numerator (1), and keep the same denominator (2). This gives us (13 * 2) + 1 = 27/2.
-
Divide the numerator by the denominator: Now, we divide the numerator (27) by the denominator (2): 27 ÷ 2 = 13.5
Again, we arrive at the decimal equivalent of 13.5.
Method 3: Using a Calculator
The simplest method, especially for more complex mixed numbers, is to use a calculator. Simply enter "13 + 1/2" or "27/2" into the calculator, and it will directly provide the decimal equivalent of 13.5.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is essential in numerous real-world situations:
-
Financial Calculations: Dealing with money often involves fractions of a currency unit (e.g., cents are fractions of a dollar). Converting these fractions to decimals simplifies calculations like calculating discounts, taxes, or interest. For example, understanding that 13 1/2 dollars is $13.50 is crucial for accurate financial transactions.
-
Measurement and Engineering: Many measurements involve fractions of units (e.g., inches, centimeters). Converting these fractions to decimals is necessary for precise calculations in fields like engineering, construction, and manufacturing. A blueprint might specify a length of 13 1/2 inches, which is easier to work with as 13.5 inches in many calculations.
-
Scientific Calculations: Science and engineering rely heavily on precise numerical representations. Converting fractions to decimals ensures accuracy in calculations and data analysis.
-
Data Analysis and Statistics: Statistical analysis often involves working with fractional data. Converting these fractions to decimals allows for easier data manipulation and interpretation using statistical software and tools.
-
Computer Programming: Computers typically work with decimal representations of numbers. Therefore, converting fractions to decimals is a necessary step in many programming tasks.
Beyond 13 1/2: Converting Other Mixed Numbers to Decimals
The methods described above can be applied to any mixed number. Let's consider a few examples:
-
5 3/4: First, convert 3/4 to a decimal (0.75). Then, add the whole number: 5 + 0.75 = 5.75
-
2 1/8: Convert 1/8 to a decimal (0.125). Then, add the whole number: 2 + 0.125 = 2.125
-
10 2/3: This one is slightly trickier because the fraction 2/3 results in a repeating decimal (0.666...). You can round it to a certain number of decimal places (e.g., 10.67) for practical purposes.
Remember to always follow the same steps: convert the fraction to a decimal and then add the whole number. For repeating decimals, you might need to make a decision on how many decimal places you want to keep for your application.
Frequently Asked Questions (FAQs)
Q1: What if the fraction is an improper fraction (numerator is larger than the denominator)?
A1: If the fraction is improper, you can still convert it to a decimal by performing the division. For example, 7/4 = 1.75. If the improper fraction is part of a mixed number, you can first convert the mixed number to an improper fraction, then divide to get the decimal.
Q2: How do I handle repeating decimals?
A2: Repeating decimals can be expressed as a fraction. For example, 0.333... is equal to 1/3. However, for practical applications, you can round the repeating decimal to a certain number of decimal places based on the required level of precision.
Q3: Are there any online tools or calculators that can help with these conversions?
A3: Yes, many online calculators and conversion tools can convert fractions to decimals. A simple web search for "fraction to decimal converter" will provide several options. However, understanding the underlying process is crucial for a deeper understanding of mathematics.
Q4: Why is it important to understand fraction to decimal conversions?
A4: Fraction to decimal conversions are vital for various applications across different fields, ensuring accuracy and efficiency in calculations, data analysis, and problem-solving. It bridges the gap between two common ways of representing numerical values.
Conclusion
Converting 13 1/2 to its decimal equivalent (13.5) is a straightforward process that involves understanding the relationship between fractions and decimals. This article has provided a detailed explanation of the various methods, practical applications, and frequently asked questions surrounding this essential mathematical concept. Mastering fraction-to-decimal conversions is a valuable skill that will improve your mathematical abilities and problem-solving skills across various disciplines. Remember that understanding the underlying principles is key, not just memorizing the steps. Through practice and application, you will develop a solid understanding and confidently navigate these conversions.
Latest Posts
Latest Posts
-
What Is The Gcf Of 20 And 24
May 25, 2025
-
421 Divided By 27 With Remainder
May 25, 2025
-
You Re Compatible With 0 Of The Female Population Test
May 25, 2025
-
What Is The Greatest Common Factor Of 26 And 52
May 25, 2025
-
What Percent Of 25 Is 3
May 25, 2025
Related Post
Thank you for visiting our website which covers about 13 1 2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.