12 Out Of 21 As A Percentage
listenit
May 24, 2025 · 5 min read
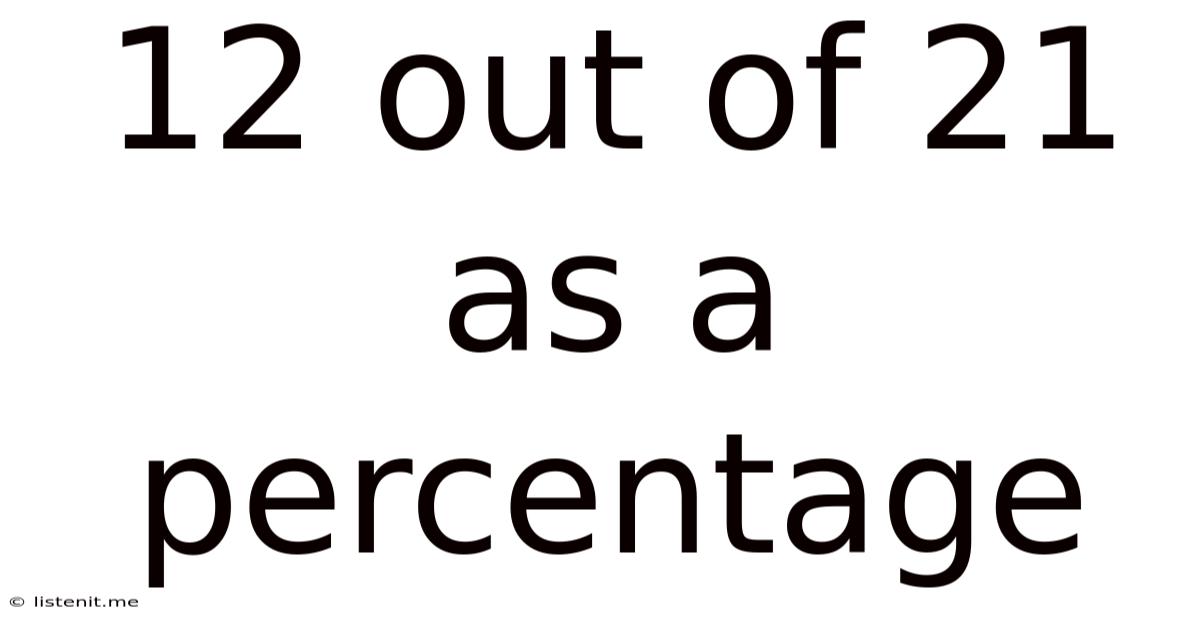
Table of Contents
12 out of 21 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex scientific analyses and financial modeling. This article delves deep into calculating percentages, using the example of "12 out of 21" to illustrate various methods and their applications. We'll move beyond the simple calculation to explore the broader context of percentage interpretation and application.
What is a Percentage?
A percentage represents a fraction of 100. It's a way to express a proportion or ratio as a number out of 100. The symbol "%" denotes a percentage. For instance, 50% means 50 out of 100, or one-half.
Calculating 12 out of 21 as a Percentage: The Basic Method
The most straightforward way to calculate 12 out of 21 as a percentage involves these steps:
-
Form a Fraction: Represent "12 out of 21" as a fraction: 12/21.
-
Convert to a Decimal: Divide the numerator (12) by the denominator (21): 12 ÷ 21 ≈ 0.5714
-
Multiply by 100: To convert the decimal to a percentage, multiply by 100: 0.5714 × 100 ≈ 57.14%
Therefore, 12 out of 21 is approximately 57.14%.
Alternative Calculation Methods
While the above method is the most common, other approaches can be used, particularly when dealing with more complex scenarios or when using calculators or spreadsheets.
-
Using Proportions: We can set up a proportion: 12/21 = x/100. Solving for 'x' gives us the percentage. Cross-multiplying, we get 21x = 1200. Dividing both sides by 21, we arrive at x ≈ 57.14.
-
Using a Calculator: Most calculators have a percentage function. Simply enter 12 ÷ 21 and then multiply by 100 to obtain the percentage directly.
-
Using Spreadsheets (e.g., Excel or Google Sheets): Spreadsheets offer built-in functions for percentage calculations. The formula
=(12/21)*100would directly give you the result.
Understanding the Significance of the Result: 57.14%
The result, 57.14%, signifies that 12 represents approximately 57.14% of the total value of 21. This percentage can be used in a variety of contexts depending on the underlying data. For example, if 21 represents the total number of students in a class, and 12 represent the number of students who passed an exam, then 57.14% is the pass rate. In another context, if 21 represents the total number of attempts and 12 represent the successful attempts, then 57.14% is the success rate.
Rounding Percentages
The calculated percentage, 57.14%, is an approximation. The level of precision needed depends on the context. Rounding to the nearest whole number (57%) is acceptable in many casual situations. However, in financial or scientific settings, more decimal places may be necessary to maintain accuracy. The appropriate level of rounding should always be clearly stated.
Applications of Percentage Calculations
Percentage calculations are essential in diverse fields:
-
Business and Finance: Calculating profit margins, interest rates, discounts, tax rates, and return on investment (ROI).
-
Science: Expressing experimental results, calculating error rates, and representing statistical data.
-
Education: Determining grades, pass rates, and student performance metrics.
-
Healthcare: Tracking disease prevalence, calculating medication dosages, and analyzing clinical trial results.
-
Everyday Life: Calculating tips, sales tax, discounts in shops, and budgeting household expenses.
Common Percentage-Related Calculations
Beyond simply finding a percentage of a whole, many other percentage-related calculations are frequently encountered. Let's explore some examples:
-
Finding a Percentage of a Number: This involves multiplying the number by the percentage (expressed as a decimal). For instance, finding 20% of 50 involves calculating 0.20 × 50 = 10.
-
Finding the Percentage Increase or Decrease: This involves calculating the difference between two values and expressing it as a percentage of the original value. For instance, if a value increases from 100 to 120, the percentage increase is (120-100)/100 × 100% = 20%.
-
Finding the Original Value after a Percentage Change: If you know the final value and the percentage change, you can work backward to find the original value. For example, if a value increased by 10% to reach 110, the original value was 110 / 1.10 = 100.
Advanced Percentage Calculations and Concepts
For more complex scenarios, advanced techniques might be necessary. These include:
-
Compound Interest: Interest calculated not only on the principal but also on the accumulated interest.
-
Percentage Points: Representing the absolute difference between two percentages, not a relative change. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Weighted Averages: Calculating the average of values where each value carries a different weight or importance.
-
Statistical Significance Testing: Used in hypothesis testing to determine the probability of observing a result if there was no real effect.
Addressing Potential Errors in Percentage Calculations
Common mistakes when working with percentages include:
-
Incorrect Order of Operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Confusing Percentage Points and Percentage Change: Remember the difference between a percentage point change and a percentage change.
-
Incorrect Rounding: Rounding at inappropriate stages of the calculation can lead to significant errors in the final result. Always round to the required level of precision at the very end.
-
Using the Wrong Base: Always clearly identify the base (the original value) when calculating percentage changes.
Conclusion: Mastering Percentage Calculations
Understanding and accurately calculating percentages is a crucial skill across various aspects of life. This article provides a comprehensive guide, using the example of "12 out of 21," demonstrating different methods and highlighting common pitfalls. By mastering these concepts and techniques, you'll enhance your ability to interpret data, make informed decisions, and excel in various quantitative tasks. Remember to practice regularly and always double-check your work to ensure accuracy. With consistent effort, you can become proficient in percentage calculations and confidently apply them in various contexts.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 48 And 42
May 25, 2025
-
3 1 7 As An Improper Fraction
May 25, 2025
-
What Is The Square Root Of 1 Million
May 25, 2025
-
What Is 3 8 Of 16
May 25, 2025
-
How To Calculate Current In Resistor
May 25, 2025
Related Post
Thank you for visiting our website which covers about 12 Out Of 21 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.