12 Of 30 Is What Percent
listenit
May 25, 2025 · 5 min read
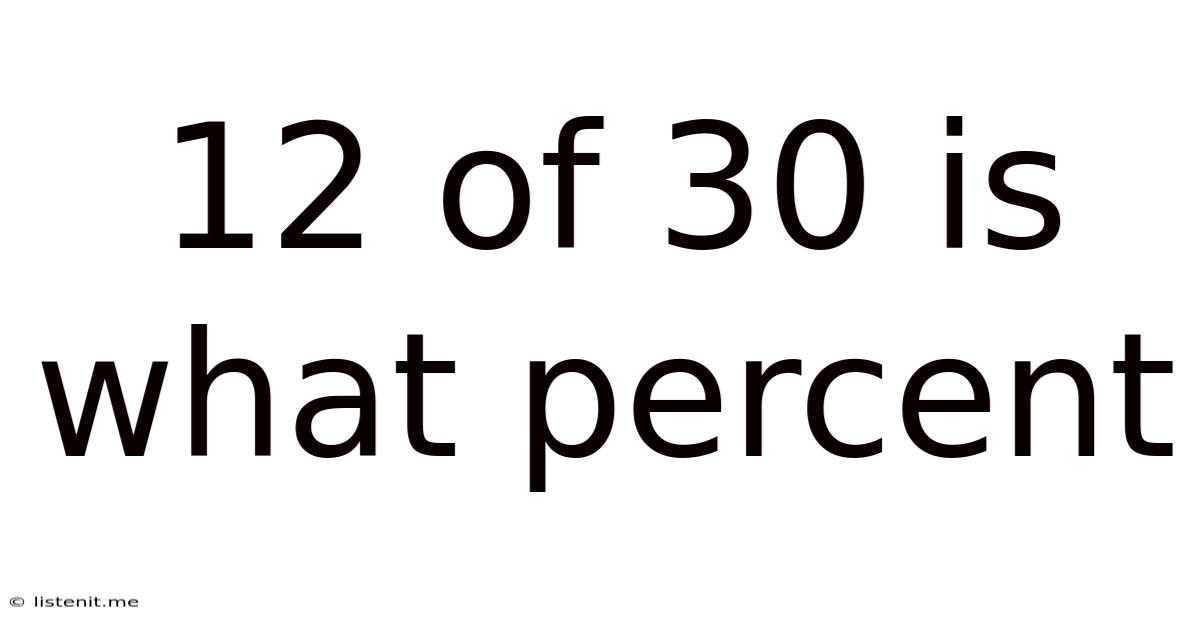
Table of Contents
12 out of 30 is What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will not only answer the question "12 out of 30 is what percent?" but also equip you with the knowledge and tools to tackle any percentage problem with confidence. We'll delve into various methods, explore practical applications, and provide you with tips and tricks to master this essential skill.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a number out of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. Understanding this basic relationship is key to solving any percentage problem.
Calculating "12 out of 30": Method 1 - The Fraction Method
The most straightforward approach to determining what percentage 12 out of 30 represents is using fractions.
-
Express the problem as a fraction: The problem "12 out of 30" can be written as the fraction 12/30.
-
Simplify the fraction: To make calculations easier, simplify the fraction by finding the greatest common divisor (GCD) of the numerator (12) and the denominator (30). The GCD of 12 and 30 is 6. Dividing both the numerator and the denominator by 6 gives us the simplified fraction 2/5.
-
Convert the fraction to a decimal: To convert the fraction 2/5 to a decimal, divide the numerator (2) by the denominator (5): 2 ÷ 5 = 0.4
-
Convert the decimal to a percentage: To convert the decimal 0.4 to a percentage, multiply it by 100: 0.4 x 100 = 40%
Therefore, 12 out of 30 is 40%.
Calculating "12 out of 30": Method 2 - The Proportion Method
The proportion method provides another way to solve percentage problems. This method is particularly useful when dealing with more complex scenarios.
-
Set up a proportion: We can express the problem as a proportion: 12/30 = x/100, where 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiply the terms to get: 30x = 1200
-
Solve for x: Divide both sides of the equation by 30: x = 1200 ÷ 30 = 40
Therefore, x = 40%, confirming that 12 out of 30 is 40%.
Calculating "12 out of 30": Method 3 - Using a Calculator
Most calculators have a percentage function that simplifies the process.
-
Divide the part by the whole: Divide 12 by 30: 12 ÷ 30 = 0.4
-
Multiply by 100: Multiply the result by 100: 0.4 x 100 = 40
-
Add the percentage symbol: The answer is 40%.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world situations. Here are a few examples:
-
Calculating Discounts: If a store offers a 20% discount on an item priced at $50, you can easily calculate the discount amount and the final price using percentage calculations.
-
Determining Sales Tax: Understanding percentages is essential for calculating the sales tax on purchases.
-
Analyzing Grades: Students use percentages to understand their academic performance based on marks obtained in exams and assignments.
-
Understanding Financial Statements: Businesses use percentages extensively in financial statements to analyze profitability, expenses, and other key metrics.
-
Interpreting Statistical Data: Percentages are frequently used in statistics to represent proportions, trends, and probabilities. For instance, understanding survey results often requires interpreting percentages.
-
Calculating Interest Rates: Percentages are fundamental to calculating simple and compound interest on loans and investments.
Beyond the Basics: More Complex Percentage Problems
While "12 out of 30 is what percent?" is a relatively simple problem, the principles can be applied to more complex scenarios. For example:
-
Finding the percentage increase or decrease: This involves calculating the percentage change between two values. For example, if a quantity increases from 50 to 60, the percentage increase is calculated as: [(60-50)/50] x 100 = 20%.
-
Calculating percentages of percentages: Sometimes, you need to calculate a percentage of another percentage. For instance, finding 15% of 20% involves multiplying the two percentages: 0.15 x 0.20 = 0.03 or 3%.
-
Working backwards from a percentage: This involves finding the original value when you know the percentage and the resulting value. For instance, if 25% of a number is 10, you can find the original number by solving the equation: 0.25x = 10, which gives x = 40.
Tips and Tricks for Mastering Percentage Calculations
-
Practice regularly: The more you practice, the more comfortable you will become with percentage calculations.
-
Use different methods: Experiment with different methods to find the approach that works best for you.
-
Visualize the problem: Draw diagrams or use visual aids to help you understand the problem better.
-
Check your work: Always check your answer to make sure it makes sense in the context of the problem.
-
Use online resources: Numerous online calculators and tutorials can help you learn and practice percentage calculations.
Conclusion: Mastering Percentages for Success
The ability to calculate percentages accurately and efficiently is a highly valuable skill. Whether you're dealing with simple problems like "12 out of 30 is what percent?" or more complex scenarios, understanding the fundamental principles and practicing regularly will enable you to confidently tackle any percentage calculation that comes your way. This skill will undoubtedly enhance your problem-solving abilities and prove invaluable across various aspects of your personal and professional life. Remember to utilize the different methods outlined, practice regularly, and leverage available resources to solidify your understanding and achieve mastery in percentage calculations.
Latest Posts
Latest Posts
-
What Is The Total Area Of The Figure
May 25, 2025
-
2 3 To The Second Power
May 25, 2025
-
Greatest Common Factor Of 10 And 30
May 25, 2025
-
How Many Years Between 1967 And 2024
May 25, 2025
-
Greatest Common Factor Of 35 And 63
May 25, 2025
Related Post
Thank you for visiting our website which covers about 12 Of 30 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.