12 Divided By Square Root Of 3
listenit
May 10, 2025 · 4 min read
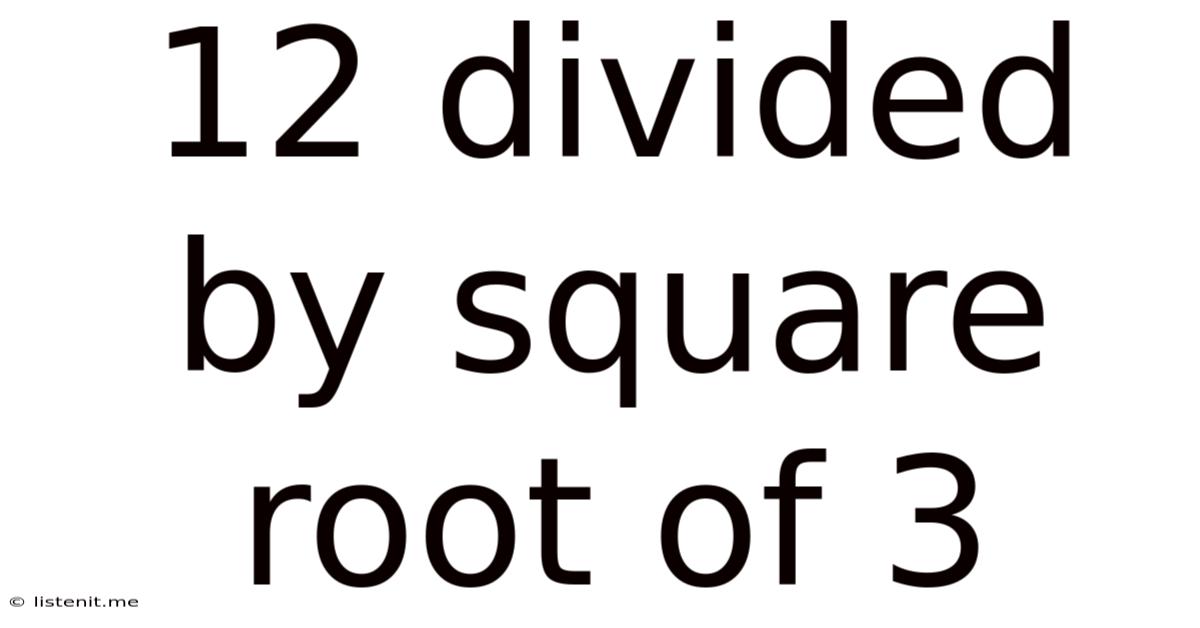
Table of Contents
12 Divided by the Square Root of 3: A Deep Dive into Simplification and Rationalization
The seemingly simple mathematical expression "12 divided by the square root of 3" (12/√3) presents a valuable opportunity to explore fundamental concepts in algebra and number theory. While a calculator can quickly provide a decimal approximation, understanding the process of simplifying and rationalizing this expression offers a deeper understanding of mathematical principles and strengthens problem-solving skills. This article will delve into the various methods for solving this problem, exploring the underlying mathematical logic and demonstrating the importance of presenting answers in their simplest, most accurate forms.
Understanding the Problem: Why Rationalization Matters
The expression 12/√3 contains an irrational denominator – the square root of 3 (√3). While this is a perfectly valid representation, mathematical convention and practical applications often prefer expressions with rational denominators. Rationalizing the denominator simplifies the expression, making it easier to work with in further calculations and providing a clearer, more easily understood representation of the value. This process doesn't change the numerical value of the expression; it merely transforms its form for improved clarity and usability.
Method 1: Direct Rationalization
The most straightforward method involves multiplying both the numerator and the denominator by the square root of 3. This technique leverages the property that multiplying a number by its square root yields the number itself (√3 * √3 = 3).
Steps:
-
Multiply the numerator and denominator by √3: (12/√3) * (√3/√3)
-
Simplify: This results in (12√3) / (√3 * √3) = (12√3) / 3
-
Further Simplification: Reduce the fraction by dividing both numerator and denominator by 3: (12√3) / 3 = 4√3
Therefore, 12 divided by the square root of 3 simplifies to 4√3. This is the preferred form as it’s concise and the denominator is rational.
Method 2: Prime Factorization and Simplification
This method uses prime factorization to simplify the expression before rationalizing. It’s particularly useful when dealing with more complex expressions.
Steps:
-
Prime Factorization of 12: 12 can be factored as 2² * 3
-
Rewrite the expression: The original expression becomes (2² * 3) / √3
-
Simplify the square root: We can rewrite √3 as 3^(1/2).
-
Combine and simplify: (2² * 3) / 3^(1/2) can be rewritten as 2² * 3^(1 - 1/2) = 2² * 3^(1/2) = 4√3
This method again arrives at the simplified answer of 4√3.
Method 3: Using the Conjugate (for more complex expressions)
While not strictly necessary for this particular problem, understanding how to use conjugates is crucial when dealing with expressions involving sums or differences of square roots. This method is particularly helpful when you have a binomial in the denominator (e.g., √3 + 1).
For example, if the problem were 12/(√3 + 1), we'd multiply both the numerator and denominator by the conjugate of the denominator (√3 - 1). The conjugate is formed by changing the sign between the terms.
Steps (example with a binomial denominator):
-
Multiply by the conjugate: [12/(√3 + 1)] * [(√3 - 1)/(√3 - 1)]
-
Expand the denominator: The denominator becomes (√3 + 1)(√3 - 1) = 3 - 1 = 2 (This utilizes the difference of squares formula: (a + b)(a - b) = a² - b²)
-
Expand the numerator: The numerator becomes 12(√3 - 1) = 12√3 - 12
-
Simplify: The final expression is (12√3 - 12)/2 = 6√3 - 6
This illustrates the power of the conjugate method for more complex expressions. However, for 12/√3, the simpler direct rationalization method is sufficient and more efficient.
Decimal Approximation and its Limitations
While 4√3 is the exact and preferred simplified form, a decimal approximation can be useful for practical applications. Using a calculator, we find that √3 ≈ 1.732. Therefore, 4√3 ≈ 4 * 1.732 = 6.928. However, it's crucial to remember that this is an approximation, and the exact value remains 4√3. Using the decimal approximation can introduce rounding errors in further calculations, so the simplified radical form is always preferable whenever possible.
Applications in Geometry and Trigonometry
Understanding how to simplify expressions like 12/√3 is essential in various fields, particularly geometry and trigonometry. For example, consider a right-angled triangle where one leg has length 12 and the hypotenuse has length 6√3. Using the Pythagorean theorem, we can find the length of the other leg and related trigonometric functions.
Expanding the Understanding: Similar Problems and Exercises
To further solidify your understanding, consider tackling similar problems involving rationalization:
- 6/√2
- 15/√5
- 20/√8
These exercises allow you to practice the techniques discussed, reinforcing your understanding of rationalization and simplifying radical expressions. Remember to always aim for the most simplified, rational form of your answer.
Conclusion: Beyond the Calculation
Solving 12/√3 is more than just a simple arithmetic exercise. It's a gateway to understanding essential mathematical concepts: rationalization, simplification, and the importance of presenting answers in their most accurate and usable form. Mastering these concepts enhances problem-solving skills and lays a strong foundation for tackling more complex mathematical challenges in various fields, from engineering and physics to computer science and finance. The ability to manipulate and simplify radical expressions is a key skill for any student pursuing advanced mathematical studies. Remember the elegance and efficiency of expressing your answer as 4√3; it's a testament to the power of mathematical precision and simplification.
Latest Posts
Latest Posts
-
A Compound Is A Combination Of Two Or More Chemicals
May 10, 2025
-
Sulfuric Acid Sodium Hydroxide Balanced Equation
May 10, 2025
-
How To Balance Na H2o Naoh H2
May 10, 2025
-
Common Multiple Of 7 And 8
May 10, 2025
-
Find The Common Factor Of 20 And 28
May 10, 2025
Related Post
Thank you for visiting our website which covers about 12 Divided By Square Root Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.