12 As A Percentage Of 15
listenit
May 09, 2025 · 5 min read
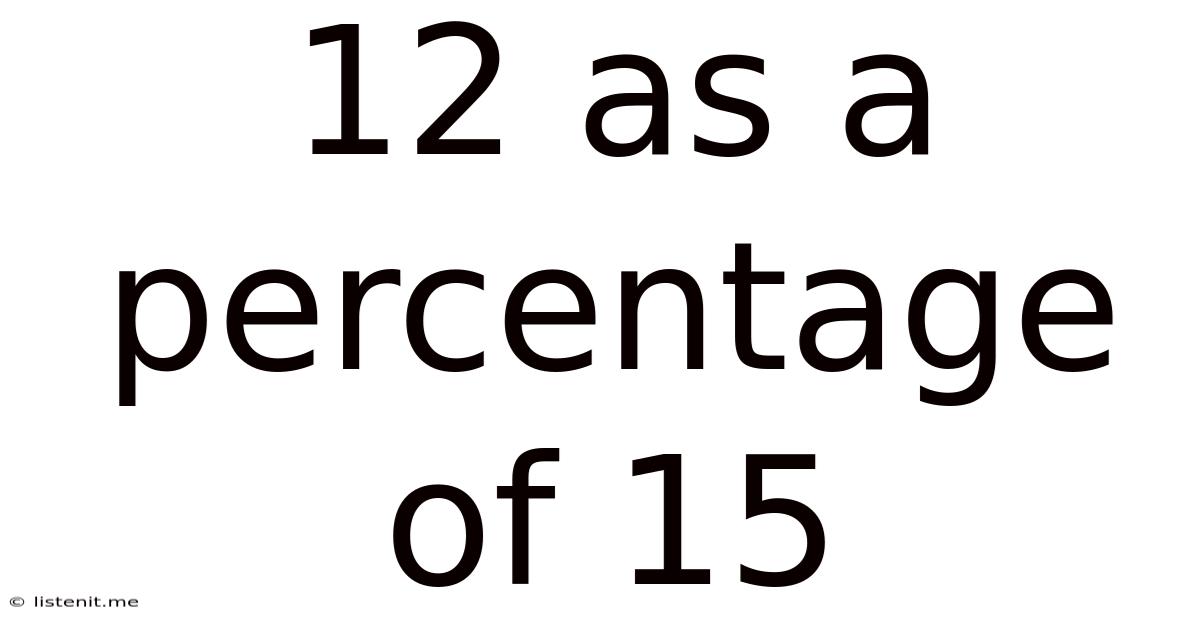
Table of Contents
12 as a Percentage of 15: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various fields, from finance and business to everyday life. Understanding how to determine one number as a percentage of another is crucial for interpreting data, making informed decisions, and solving numerous practical problems. This article delves deep into calculating 12 as a percentage of 15, providing a step-by-step explanation, exploring different methods, and offering practical examples to solidify your understanding. We'll also examine the broader context of percentage calculations and their importance.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, a percentage represents a portion or proportion of a whole. For example, 50% means 50 out of 100, or one-half.
Calculating 12 as a Percentage of 15: The Basic Method
The most straightforward way to calculate 12 as a percentage of 15 involves three simple steps:
-
Divide the part by the whole: In this case, the "part" is 12, and the "whole" is 15. Therefore, we divide 12 by 15: 12 ÷ 15 = 0.8
-
Multiply the result by 100: To convert the decimal to a percentage, we multiply the result from step 1 by 100: 0.8 x 100 = 80
-
Add the percentage symbol: Finally, we add the percentage symbol (%) to indicate that the result is a percentage: 80%
Therefore, 12 is 80% of 15.
Alternative Method: Using Proportions
Another way to approach this problem is by setting up a proportion. A proportion is a statement of equality between two ratios. We can express the problem as:
12/15 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
15x = 1200
Then, divide both sides by 15:
x = 1200 ÷ 15 = 80
Therefore, x = 80%, confirming our previous result.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world scenarios. Here are a few examples:
-
Calculating Discounts: If a store offers a 20% discount on an item priced at $50, you can easily calculate the discount amount and the final price using percentage calculations.
-
Determining Grades: Many grading systems use percentages to represent a student's performance on tests and assignments. Understanding percentages helps students track their progress and understand their overall performance.
-
Analyzing Financial Statements: Businesses utilize percentage calculations to analyze financial data, such as profit margins, revenue growth, and expense ratios. This information is crucial for making sound financial decisions.
-
Understanding Statistics: Percentages are frequently used in presenting statistical data, making it easier to understand and compare different sets of information. For example, understanding unemployment rates, population growth, and market share all rely on percentage calculations.
-
Calculating Taxes: Tax calculations heavily involve percentages. Understanding tax rates and how they apply to different income brackets requires a solid grasp of percentage calculations.
-
Cooking and Baking: Many recipes use percentages to describe the proportion of ingredients. For example, a recipe might call for 60% flour and 40% water. Accurate percentage calculation ensures consistent results.
Expanding on Percentage Calculations: Further Exploration
While the example of 12 as a percentage of 15 is relatively straightforward, the principles involved can be applied to more complex scenarios. Here are some points to consider:
-
Calculating the Whole: If you know the percentage and the part, you can calculate the whole. For example, if 25% of a number is 10, you can calculate the whole number using the equation: (10/25) * 100 = 40.
-
Calculating the Part: If you know the percentage and the whole, you can calculate the part. For example, if 75% of 60 is X, then X= (75/100) * 60 = 45.
-
Percentage Increase and Decrease: Calculating percentage increase or decrease requires finding the difference between two numbers and expressing that difference as a percentage of the original number. This is a crucial concept in finance, economics, and statistics.
-
Compound Interest: Compound interest involves calculating interest not only on the principal amount but also on accumulated interest. This calculation requires multiple percentage calculations and demonstrates the power of exponential growth.
Advanced Percentage Calculations and Applications
Moving beyond basic percentage calculations opens up a world of sophisticated applications:
-
Statistical Analysis: Percentages are fundamental in statistical analysis for summarizing and interpreting data, identifying trends, and making inferences. Techniques like hypothesis testing and confidence intervals often utilize percentage calculations.
-
Financial Modeling: Financial models rely heavily on percentage calculations to forecast future performance, assess risk, and optimize investment strategies. These models use complex formulas incorporating percentages to simulate various economic scenarios.
-
Data Visualization: Percentages are frequently used in data visualization, such as pie charts and bar graphs, to represent proportions of a whole and make complex data sets more accessible and understandable.
-
Machine Learning: While not directly using percentages in the same way, machine learning algorithms often utilize probabilistic models, which are closely related to percentages and probabilities. These models use percentage-like values to predict outcomes and make classifications.
Conclusion: Mastering Percentage Calculations for Success
Mastering percentage calculations is a valuable skill that extends far beyond basic arithmetic. It equips you with the tools necessary to interpret data, make informed decisions, and excel in various fields. By understanding the fundamental principles and exploring various methods of calculation, you can confidently tackle percentage problems of varying complexity. Remember, the ability to confidently work with percentages opens doors to deeper understanding in numerous disciplines, from finance to everyday life. Continuously practicing and applying these techniques will further solidify your understanding and build your analytical skills. This understanding not only improves practical problem-solving capabilities, but also fosters critical thinking and enhances your overall analytical abilities.
Latest Posts
Latest Posts
-
5 Is What Percent Of 100
May 09, 2025
-
Find The Exact Value Of Sin 105
May 09, 2025
-
How To Turn Off Scientific Notation On Ti 84 Plus
May 09, 2025
-
Exterior Angle Of A Regular Hexagon
May 09, 2025
-
Is Corrosion A Physical Or Chemical Change
May 09, 2025
Related Post
Thank you for visiting our website which covers about 12 As A Percentage Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.