12 And A Half As A Fraction
listenit
May 21, 2025 · 5 min read
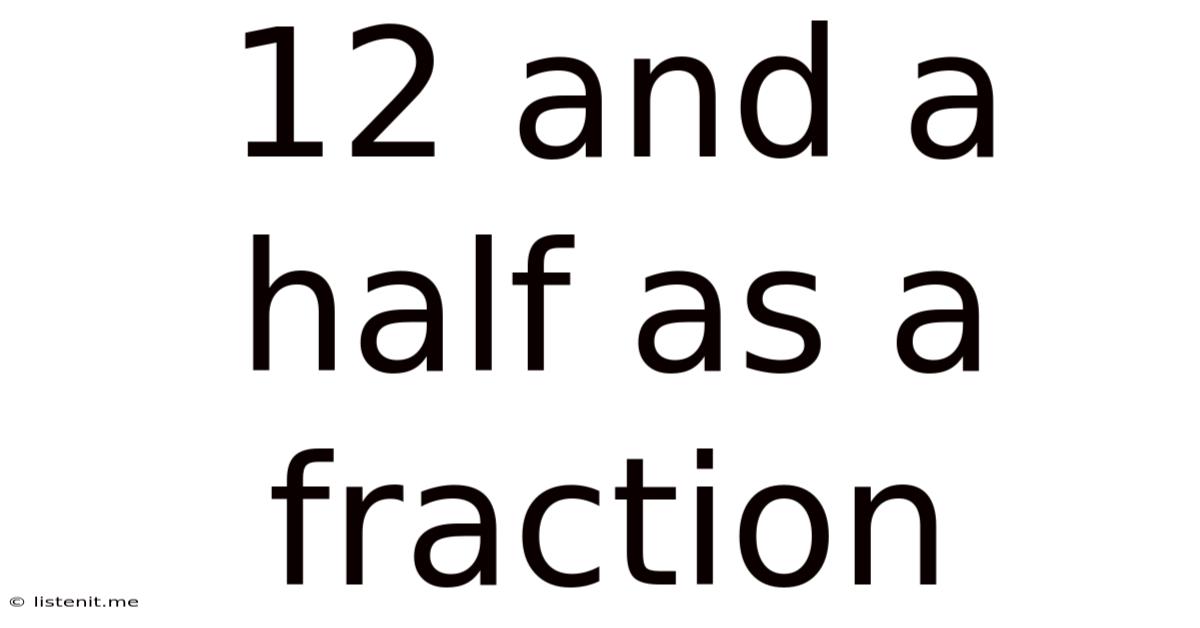
Table of Contents
12 and a Half as a Fraction: A Comprehensive Guide
Understanding fractions is a cornerstone of mathematics, impacting various aspects of our lives, from baking to construction. This comprehensive guide delves into the seemingly simple yet multifaceted topic of representing "12 and a half" as a fraction. We'll explore different approaches, unravel the underlying concepts, and highlight practical applications. This detailed explanation aims to solidify your understanding and equip you with the tools to tackle similar fractional conversions with confidence.
Understanding Mixed Numbers and Improper Fractions
Before diving into the conversion, let's establish a clear understanding of the terminology involved. "12 and a half" is a mixed number. A mixed number combines a whole number (12 in this case) and a fraction (1/2). Conversely, an improper fraction has a numerator (top number) larger than or equal to its denominator (bottom number). Converting between mixed numbers and improper fractions is crucial for various mathematical operations.
Why Convert to an Improper Fraction?
While mixed numbers are easily understandable, improper fractions are often necessary for calculations involving multiplication and division of fractions. They provide a more streamlined approach to these operations, avoiding the complexities of working with whole numbers and fractions simultaneously.
Converting 12 and a Half to an Improper Fraction: Step-by-Step
The conversion process involves two simple steps:
-
Multiply the whole number by the denominator: In our case, this is 12 (whole number) multiplied by 2 (denominator of the fraction). This results in 24.
-
Add the numerator: Add the result from step 1 (24) to the numerator of the original fraction (1). This gives us 25.
-
Keep the denominator the same: The denominator remains unchanged at 2.
Therefore, 12 and a half expressed as an improper fraction is 25/2.
Visualizing 12 and a Half
Imagine you have 12 complete pizzas and half a pizza. To represent this as a fraction, we need a common unit. Think of slicing each of the 12 pizzas into 2 equal pieces. You'll now have 24 slices (12 pizzas x 2 slices/pizza). Adding the half-pizza slice, you have a total of 25 slices. Since each pizza was divided into 2 slices, the denominator remains 2, giving us the improper fraction 25/2.
Practical Applications of 12 and a Half as a Fraction
The ability to convert mixed numbers into improper fractions is vital in various real-world scenarios:
-
Baking and Cooking: Recipe conversions often require working with fractions. Scaling a recipe up or down necessitates comfortable manipulation of fractions.
-
Construction and Engineering: Precise measurements are paramount in construction. Converting mixed numbers to improper fractions allows for accurate calculations related to lengths, volumes, and areas.
-
Finance: Calculating interest, discounts, and proportions often involves fractional calculations. Expressing values as improper fractions simplifies these computations.
-
Data Analysis: Statistical analysis frequently utilizes fractions and proportions. Representing data using improper fractions provides a consistent and efficient format for calculations.
Equivalent Fractions: Exploring Alternatives
While 25/2 is the simplest improper fraction representation of 12 and a half, it's crucial to understand the concept of equivalent fractions. An equivalent fraction maintains the same value as the original fraction, but with a different numerator and denominator. For instance, multiplying both the numerator and the denominator of 25/2 by 2 results in 50/4, which is an equivalent fraction, still representing 12 and a half. Similarly, multiplying by 3 gives 75/6, and so on.
This concept highlights that a single value can have multiple fractional representations. The simplest form, however, is generally preferred for clarity and ease of calculation.
Further Exploration: Decimal Representation
It's worthwhile to note that 12 and a half can also be represented as a decimal: 12.5. This representation is often used in everyday applications where precision beyond the nearest half isn't required. The decimal form is easily obtained by dividing the numerator of the improper fraction (25) by its denominator (2).
Troubleshooting Common Mistakes
The most frequent errors when converting mixed numbers to improper fractions involve incorrect multiplication or addition:
-
Forgetting to add the numerator: This leads to an underestimation of the value. Always remember to add the numerator after multiplying the whole number by the denominator.
-
Incorrect multiplication: Double-check your multiplication to ensure accuracy. A small error here can significantly affect the final result.
-
Using the wrong denominator: The denominator of the improper fraction must be the same as the denominator of the original fraction. Using a different denominator results in an incorrect value.
Practice Problems
To reinforce understanding, try converting these mixed numbers to improper fractions:
- 3 and ¾
- 5 and 2/5
- 1 and 1/8
- 7 and 1/3
- 10 and 5/6
Solutions are provided at the end of this article to allow for self-assessment and learning.
Conclusion: Mastering Fractions for Enhanced Mathematical Skills
Understanding how to convert mixed numbers like "12 and a half" into improper fractions is a fundamental skill with wide-ranging applications. This detailed guide provides a step-by-step process, visual aids, and practical examples to solidify your grasp of this essential mathematical concept. By mastering this skill, you'll improve your abilities in various mathematical disciplines and real-world scenarios requiring precise fractional calculations.
Solutions to Practice Problems:
- 3 and ¾ = 15/4
- 5 and 2/5 = 27/5
- 1 and 1/8 = 9/8
- 7 and 1/3 = 22/3
- 10 and 5/6 = 65/6
Latest Posts
Latest Posts
-
Likelihood Of Tongue Cancer Recurrence After 3 Years
Jun 05, 2025
-
Vesicant Blister Agents Include All Of The Following Except
Jun 05, 2025
-
Selective Caries Removal With A Pulp Cap
Jun 05, 2025
-
Upper Pole Of Kidney On Ultrasound
Jun 05, 2025
-
Giant Cell Tumor Of Bone Histology
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 12 And A Half As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.