11 Of 15 Is What Percent
listenit
May 09, 2025 · 4 min read
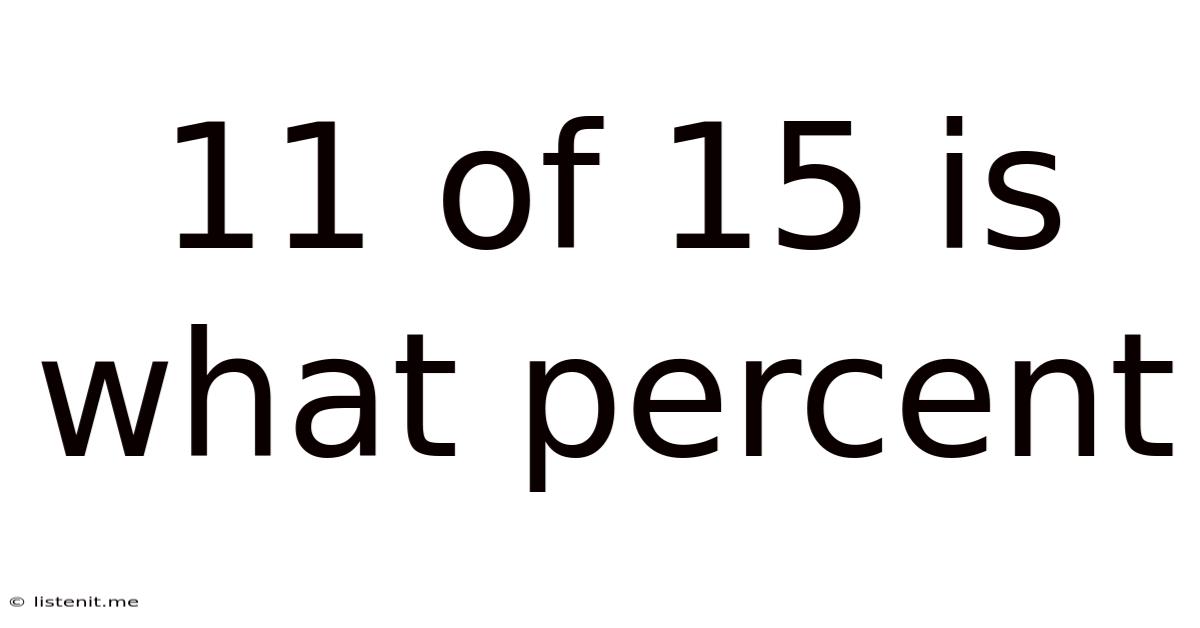
Table of Contents
11 out of 15: What Percent? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill in many areas of life, from calculating discounts and tips to analyzing data and understanding financial reports. This article will delve into the calculation of "11 out of 15 is what percent?", providing a comprehensive explanation of the process, exploring various methods, and offering practical examples to solidify your understanding. We'll also touch upon the broader applications of percentage calculations and how to avoid common pitfalls.
Understanding the Basics of Percentages
Before diving into the specific calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol used to represent percentage is "%". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating "11 out of 15 is what percent?" - Method 1: The Proportion Method
This is perhaps the most intuitive method. We can set up a proportion to solve this problem:
11/15 = x/100
Where:
- 11/15 represents the fraction of 11 out of 15.
- x/100 represents the unknown percentage (x) we want to find.
To solve for x, we cross-multiply:
11 * 100 = 15 * x
1100 = 15x
Now, divide both sides by 15:
x = 1100 / 15
x ≈ 73.33
Therefore, 11 out of 15 is approximately 73.33%.
Calculating "11 out of 15 is what percent?" - Method 2: The Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
-
Convert the fraction to a decimal: Divide 11 by 15: 11 ÷ 15 ≈ 0.7333
-
Multiply the decimal by 100: 0.7333 * 100 = 73.33
Therefore, using the decimal method, we again arrive at approximately 73.33%.
Rounding and Precision
In both methods, we encountered a repeating decimal (0.7333...). The level of precision you need depends on the context. For many applications, rounding to two decimal places (73.33%) is sufficient. However, in situations requiring higher accuracy, you might choose to round to more decimal places or use the exact fraction (11/15).
Practical Applications of Percentage Calculations
Understanding percentage calculations has a wide range of practical applications across various fields:
Finance and Economics:
- Calculating interest rates: Understanding how interest is calculated on loans, savings accounts, and investments.
- Analyzing financial statements: Interpreting financial ratios and performance indicators expressed as percentages.
- Calculating discounts and sales tax: Determining the final price of goods after discounts and taxes are applied.
- Investment returns: Measuring the profitability of investments over time.
Science and Statistics:
- Data analysis: Presenting data using percentages to show proportions and trends.
- Probability and statistics: Calculating probabilities and statistical significance, which often involve percentages.
- Scientific experiments: Expressing experimental results as percentages of success or failure.
Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants or for service providers.
- Understanding discounts: Making informed decisions when shopping and comparing prices.
- Budgeting: Tracking expenses and allocating resources based on percentages of income.
- Comparing prices: Determining which product or service offers better value.
Avoiding Common Mistakes in Percentage Calculations
While percentage calculations are relatively straightforward, several common mistakes can lead to inaccurate results:
- Incorrect order of operations: Always follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiple operations.
- Confusing percentages with decimals: Remember to convert decimals to percentages by multiplying by 100, and vice versa, by dividing by 100.
- Rounding errors: Be mindful of rounding errors, especially when performing multiple calculations. Try to work with the exact values as long as possible before rounding.
- Incorrect interpretation of percentages: Clearly understand what the percentage refers to (e.g., percentage increase versus percentage of total).
Advanced Percentage Calculations: Percentage Change and Percentage Points
While the above examples cover basic percentage calculations, it's also important to understand more advanced concepts such as percentage change and percentage points.
Percentage Change: This refers to the relative change between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100
For example, if a price increases from $10 to $12, the percentage change is:
[(12 - 10) / 10] * 100 = 20%
Percentage Points: This refers to the absolute difference between two percentages. It's not a relative change but a direct difference. For example, if the unemployment rate increases from 5% to 8%, the increase is 3 percentage points, not 3%.
Understanding the distinction between percentage change and percentage points is crucial for accurate interpretation of data.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that enhances your abilities in various aspects of life. By understanding the fundamental principles, different methods of calculation, and potential pitfalls, you can confidently tackle percentage problems and make informed decisions based on numerical data. Remember to practice regularly to solidify your understanding and apply your knowledge to real-world scenarios. Through consistent practice and a clear understanding of the concepts explained above, you can confidently navigate the world of percentages. Remember to always check your work and consider the context of your calculations to ensure accuracy and effective communication of your findings.
Latest Posts
Latest Posts
-
15 Degrees Celsius Equals What In Fahrenheit
May 10, 2025
-
For Every Atom Of Carbon In A Carbohydrate
May 10, 2025
-
Distinguish Among A Suspension A Colloid And A Solution
May 10, 2025
-
What Is The Difference Between Foliated And Nonfoliated Metamorphic Rock
May 10, 2025
-
Can A Right Triangle Have An Obtuse Angle
May 10, 2025
Related Post
Thank you for visiting our website which covers about 11 Of 15 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.